Gradient Descent based Weight Learning for Grouping Problems: Application on Graph Coloring and Equitable Graph Coloring

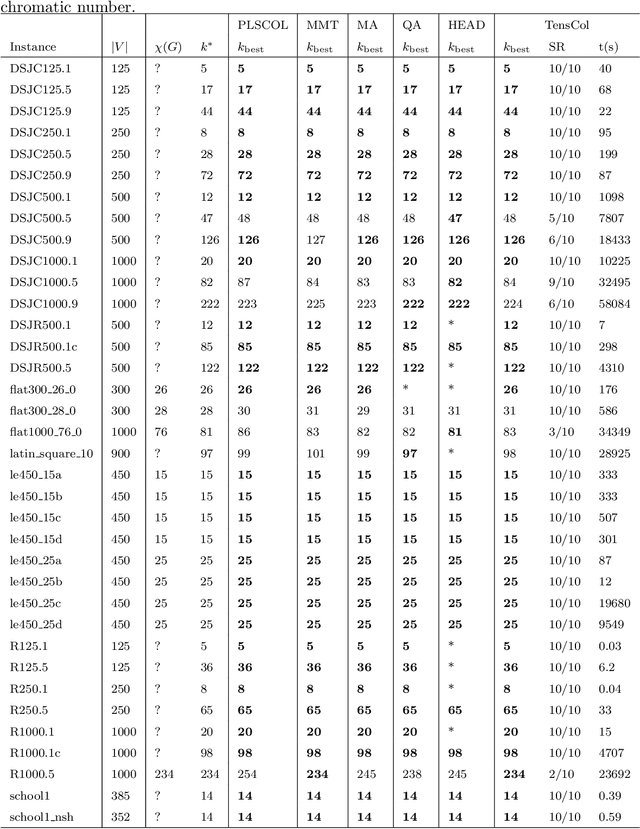
A grouping problem involves partitioning a set of items into mutually disjoint groups or clusters according to some guiding decision criteria and imperative constraints. Grouping problems have many relevant applications and are computationally difficult. In this work, we present a general weight learning based optimization framework for solving grouping problems. The central idea of our approach is to formulate the task of seeking a solution as a real-valued weight matrix learning problem that is solved by first order gradient descent. A practical implementation of this framework is proposed with tensor calculus in order to benefit from parallel computing on GPU devices. To show its potential for tackling difficult problems, we apply the approach to two typical and well-known grouping problems (graph coloring and equitable graph coloring). We present large computational experiments and comparisons on popular benchmarks and report improved best-known results (new upper bounds) for several large graphs.

Reinforcement learning based local search for grouping problems: A case study on graph coloring

Grouping problems aim to partition a set of items into multiple mutually disjoint subsets according to some specific criterion and constraints. Grouping problems cover a large class of important combinatorial optimization problems that are generally computationally difficult. In this paper, we propose a general solution approach for grouping problems, i.e., reinforcement learning based local search (RLS), which combines reinforcement learning techniques with descent-based local search. The viability of the proposed approach is verified on a well-known representative grouping problem (graph coloring) where a very simple descent-based coloring algorithm is applied. Experimental studies on popular DIMACS and COLOR02 benchmark graphs indicate that RLS achieves competitive performances compared to a number of well-known coloring algorithms.