Deinterleaving of Discrete Renewal Process Mixtures with Application to Electronic Support Measures

In this paper, we propose a new deinterleaving method for mixtures of discrete renewal Markov chains. This method relies on the maximization of a penalized likelihood score. It exploits all available information about both the sequence of the different symbols and their arrival times. A theoretical analysis is carried out to prove that minimizing this score allows to recover the true partition of symbols in the large sample limit, under mild conditions on the component processes. This theoretical analysis is then validated by experiments on synthetic data. Finally, the method is applied to deinterleave pulse trains received from different emitters in a RESM (Radar Electronic Support Measurements) context and we show that the proposed method competes favorably with state-of-the-art methods on simulated warfare datasets.

Finding optimal Pulse Repetion Intervals with Many-objective Evolutionary Algorithms

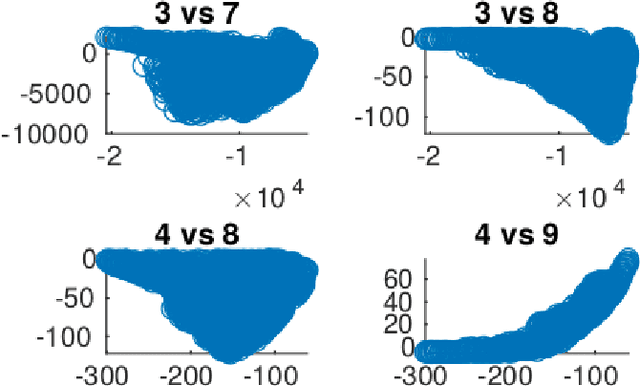
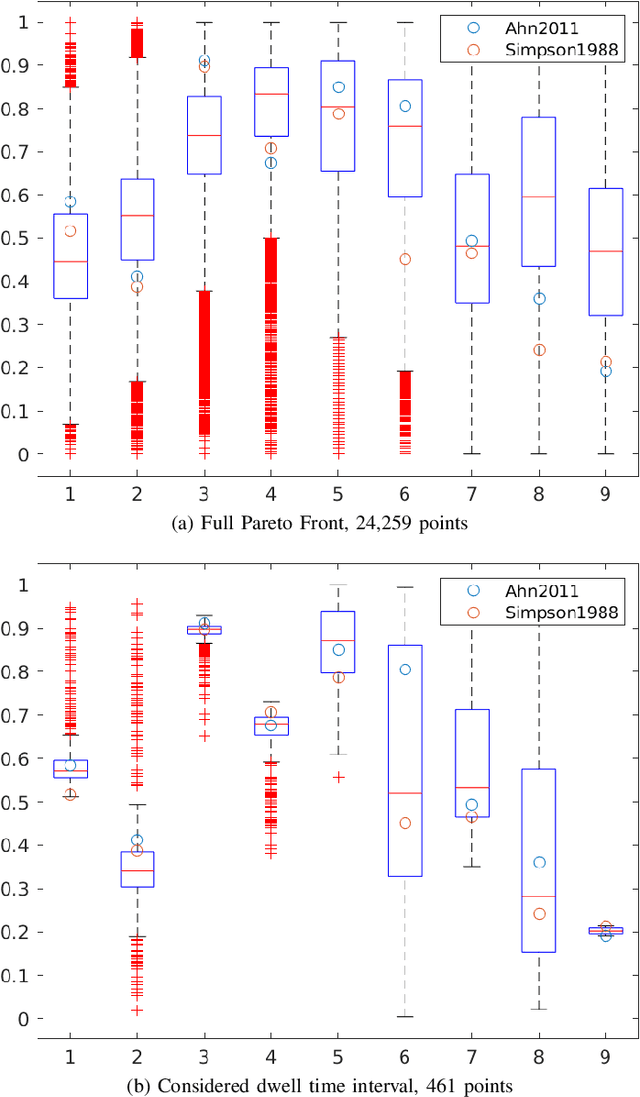
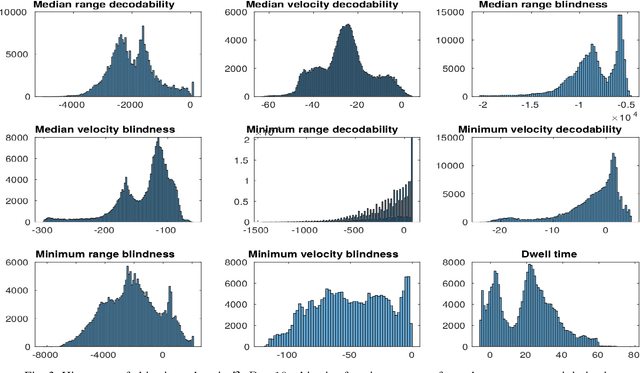
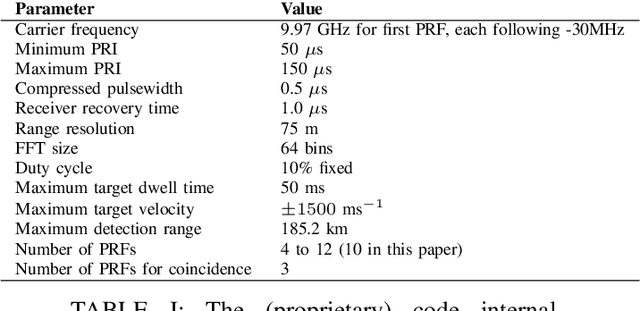
In this paper we consider the problem of finding Pulse Repetition Intervals allowing the best compromises mitigating range and Doppler ambiguities in a Pulsed-Doppler radar system. We revisit a problem that was proposed to the Evolutionary Computation community as a real-world case to test Many-objective Optimization algorithms. We use it as a baseline to compare several Evolutionary Algorithms for black-box optimization with different metrics. Resulting data is aggregated to build a reference set of Pareto optimal points and is the starting point for further analysis and operational use by the radar designer.

A generalized multivariate Student-t mixture model for Bayesian classification and clustering of radar waveforms

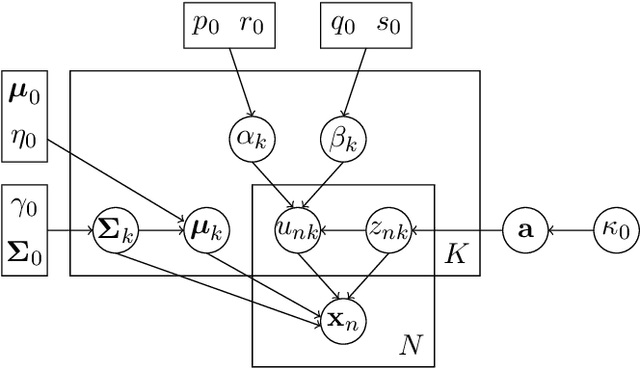
In this paper, a generalized multivariate Student-t mixture model is developed for classification and clustering of Low Probability of Intercept radar waveforms. A Low Probability of Intercept radar signal is characterized by a pulse compression waveform which is either frequency-modulated or phase-modulated. The proposed model can classify and cluster different modulation types such as linear frequency modulation, non linear frequency modulation, polyphase Barker, polyphase P1, P2, P3, P4, Frank and Zadoff codes. The classification method focuses on the introduction of a new prior distribution for the model hyper-parameters that gives us the possibility to handle sensitivity of mixture models to initialization and to allow a less restrictive modeling of data. Inference is processed through a Variational Bayes method and a Bayesian treatment is adopted for model learning, supervised classification and clustering. Moreover, the novel prior distribution is not a well-known probability distribution and both deterministic and stochastic methods are employed to estimate its expectations. Some numerical experiments show that the proposed method is less sensitive to initialization and provides more accurate results than the previous state of the art mixture models.