Model Based and Physics Informed Deep Learning Neural Network Structures

Neural Networks (NN) has been used in many areas with great success. When a NN's structure (Model) is given, during the training steps, the parameters of the model are determined using an appropriate criterion and an optimization algorithm (Training). Then, the trained model can be used for the prediction or inference step (Testing). As there are also many hyperparameters, related to the optimization criteria and optimization algorithms, a validation step is necessary before its final use. One of the great difficulties is the choice of the NN's structure. Even if there are many "on the shelf" networks, selecting or proposing a new appropriate network for a given data, signal or image processing, is still an open problem. In this work, we consider this problem using model based signal and image processing and inverse problems methods. We classify the methods in five classes, based on: i) Explicit analytical solutions, ii) Transform domain decomposition, iii) Operator Decomposition, iv) Optimization algorithms unfolding, and v) Physics Informed NN methods (PINN). Few examples in each category are explained.

Dynamical System Identification, Model Selection and Model Uncertainty Quantification by Bayesian Inference

This study presents a Bayesian maximum \textit{a~posteriori} (MAP) framework for dynamical system identification from time-series data. This is shown to be equivalent to a generalized zeroth-order Tikhonov regularization, providing a rational justification for the choice of the residual and regularization terms, respectively, from the negative logarithms of the likelihood and prior distributions. In addition to the estimation of model coefficients, the Bayesian interpretation gives access to the full apparatus for Bayesian inference, including the ranking of models, the quantification of model uncertainties and the estimation of unknown (nuisance) hyperparameters. Two Bayesian algorithms, joint maximum \textit{a~posteriori} (JMAP) and variational Bayesian approximation (VBA), are compared to the popular SINDy algorithm for thresholded least-squares regression, by application to several dynamical systems with added noise. For multivariate Gaussian likelihood and prior distributions, the Bayesian formulation gives Gaussian posterior and evidence distributions, in which the numerator terms can be expressed in terms of the Mahalanobis distance or ``Gaussian norm'' $||\vy-\hat{\vy}||^2_{M^{-1}} = (\vy-\hat{\vy})^\top {M^{-1}} (\vy-\hat{\vy})$, where $\vy$ is a vector variable, $\hat{\vy}$ is its estimator and $M$ is the covariance matrix. The posterior Gaussian norm is shown to provide a robust metric for quantitative model selection.

Deep Learning and Inverse Problems

Machine Learning (ML) methods and tools have gained great success in many data, signal, image and video processing tasks, such as classification, clustering, object detection, semantic segmentation, language processing, Human-Machine interface, etc. In computer vision, image and video processing, these methods are mainly based on Neural Networks (NN) and in particular Convolutional NN (CNN), and more generally Deep NN. Inverse problems arise anywhere we have indirect measurement. As, in general, those inverse problems are ill-posed, to obtain satisfactory solutions for them needs prior information. Different regularization methods have been proposed, where the problem becomes the optimization of a criterion with a likelihood term and a regularization term. The main difficulty, however, in great dimensional real applications, remains the computational cost. Using NN, and in particular Deep Learning (DL) surrogate models and approximate computation, can become very helpful. In this work, we focus on NN and DL particularly adapted for inverse problems. We consider two cases: First the case where the forward operator is known and used as physics constraint, the second more general data driven DL methods.

Deep Learning and Bayesian inference for Inverse Problems

Inverse problems arise anywhere we have indirect measurement. As, in general they are ill-posed, to obtain satisfactory solutions for them needs prior knowledge. Classically, different regularization methods and Bayesian inference based methods have been proposed. As these methods need a great number of forward and backward computations, they become costly in computation, in particular, when the forward or generative models are complex and the evaluation of the likelihood becomes very costly. Using Deep Neural Network surrogate models and approximate computation can become very helpful. However, accounting for the uncertainties, we need first understand the Bayesian Deep Learning and then, we can see how we can use them for inverse problems. In this work, we focus on NN, DL and more specifically the Bayesian DL particularly adapted for inverse problems. We first give details of Bayesian DL approximate computations with exponential families, then we will see how we can use them for inverse problems. We consider two cases: First the case where the forward operator is known and used as physics constraint, the second more general data driven DL methods. keyword: Neural Network, Variational Bayesian inference, Bayesian Deep Learning (DL), Inverse problems, Physics based DL.

A generalized multivariate Student-t mixture model for Bayesian classification and clustering of radar waveforms

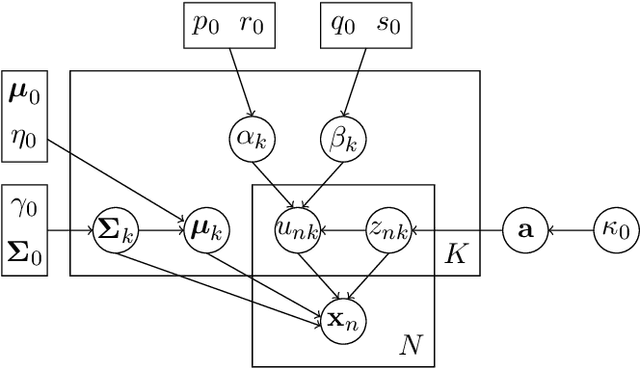
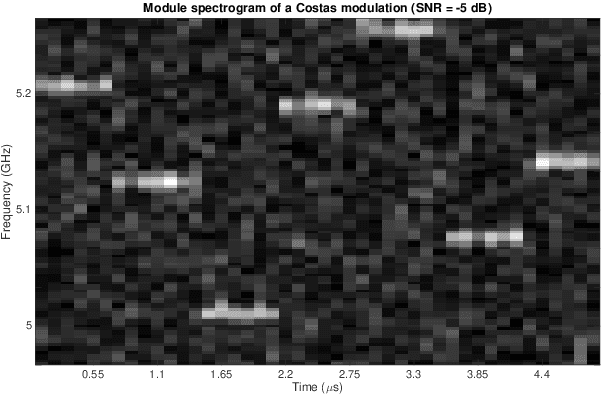
In this paper, a generalized multivariate Student-t mixture model is developed for classification and clustering of Low Probability of Intercept radar waveforms. A Low Probability of Intercept radar signal is characterized by a pulse compression waveform which is either frequency-modulated or phase-modulated. The proposed model can classify and cluster different modulation types such as linear frequency modulation, non linear frequency modulation, polyphase Barker, polyphase P1, P2, P3, P4, Frank and Zadoff codes. The classification method focuses on the introduction of a new prior distribution for the model hyper-parameters that gives us the possibility to handle sensitivity of mixture models to initialization and to allow a less restrictive modeling of data. Inference is processed through a Variational Bayes method and a Bayesian treatment is adopted for model learning, supervised classification and clustering. Moreover, the novel prior distribution is not a well-known probability distribution and both deterministic and stochastic methods are employed to estimate its expectations. Some numerical experiments show that the proposed method is less sensitive to initialization and provides more accurate results than the previous state of the art mixture models.