Private GPTs for LLM-driven testing in software development and machine learning

In this contribution, we examine the capability of private GPTs to automatically generate executable test code based on requirements. More specifically, we use acceptance criteria as input, formulated as part of epics, or stories, which are typically used in modern development processes. This gives product owners, or business intelligence, respectively, a way to directly produce testable criteria through the use of LLMs. We explore the quality of the so-produced tests in two ways: i) directly by letting the LLM generate code from requirements, ii) through an intermediate step using Gherkin syntax. As a result, it turns out that the two-step procedure yields better results -where we define better in terms of human readability and best coding practices, i.e. lines of code and use of additional libraries typically used in testing. Concretely, we evaluate prompt effectiveness across two scenarios: a simple "Hello World" program and a digit classification model, showing that structured prompts lead to higher-quality test outputs.

Dynamical System Identification, Model Selection and Model Uncertainty Quantification by Bayesian Inference

This study presents a Bayesian maximum \textit{a~posteriori} (MAP) framework for dynamical system identification from time-series data. This is shown to be equivalent to a generalized zeroth-order Tikhonov regularization, providing a rational justification for the choice of the residual and regularization terms, respectively, from the negative logarithms of the likelihood and prior distributions. In addition to the estimation of model coefficients, the Bayesian interpretation gives access to the full apparatus for Bayesian inference, including the ranking of models, the quantification of model uncertainties and the estimation of unknown (nuisance) hyperparameters. Two Bayesian algorithms, joint maximum \textit{a~posteriori} (JMAP) and variational Bayesian approximation (VBA), are compared to the popular SINDy algorithm for thresholded least-squares regression, by application to several dynamical systems with added noise. For multivariate Gaussian likelihood and prior distributions, the Bayesian formulation gives Gaussian posterior and evidence distributions, in which the numerator terms can be expressed in terms of the Mahalanobis distance or ``Gaussian norm'' $||\vy-\hat{\vy}||^2_{M^{-1}} = (\vy-\hat{\vy})^\top {M^{-1}} (\vy-\hat{\vy})$, where $\vy$ is a vector variable, $\hat{\vy}$ is its estimator and $M$ is the covariance matrix. The posterior Gaussian norm is shown to provide a robust metric for quantitative model selection.

Explainable Machine Learning Control -- robust control and stability analysis

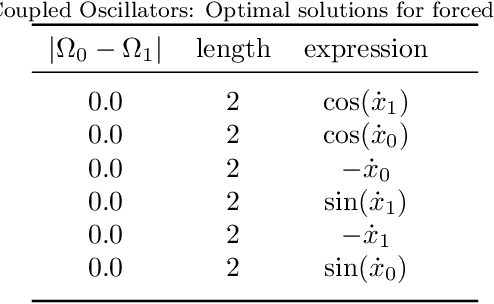
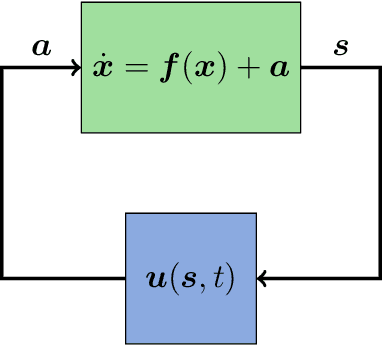
Recently, the term explainable AI became known as an approach to produce models from artificial intelligence which allow interpretation. Since a long time, there are models of symbolic regression in use that are perfectly explainable and mathematically tractable: in this contribution we demonstrate how to use symbolic regression methods to infer the optimal control of a dynamical system given one or several optimization criteria, or cost functions. In previous publications, network control was achieved by automatized machine learning control using genetic programming. Here, we focus on the subsequent analysis of the analytical expressions which result from the machine learning. In particular, we use AUTO to analyze the stability properties of the controlled oscillator system which served as our model. As a result, we show that there is a considerable advantage of explainable models over less accessible neural networks.

Inferring the dynamics of oscillatory systems using recurrent neural networks

We investigate the predictive power of recurrent neural networks for oscillatory systems not only on the attractor, but in its vicinity as well. For this we consider systems perturbed by an external force. This allows us to not merely predict the time evolution of the system, but also study its dynamical properties, such as bifurcations, dynamical response curves, characteristic exponents etc. It is shown that they can be effectively estimated even in some regions of the state space where no input data were given. We consider several different oscillatory examples, including self-sustained, excitatory, time-delay and chaotic systems. Furthermore, with a statistical analysis we assess the amount of training data required for effective inference for two common recurrent neural network cells, the long short-term memory and the gated recurrent unit.

Glyph: Symbolic Regression Tools

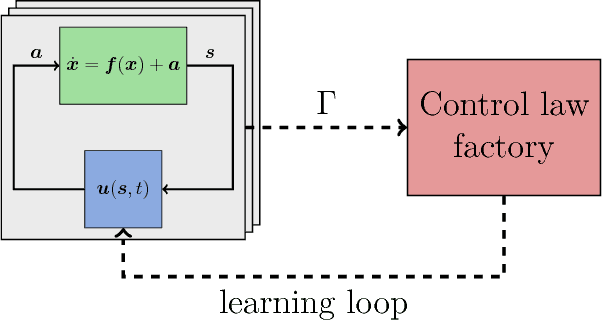
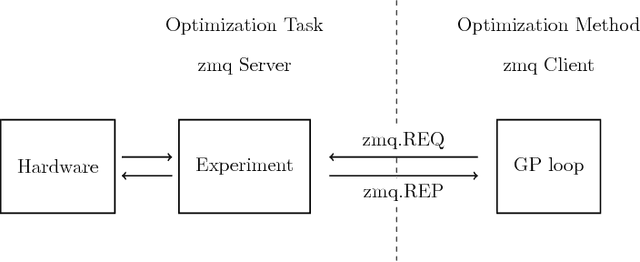
We present Glyph - a Python package for genetic programming based symbolic regression. Glyph is designed for usage let by numerical simulations let by real world experiments. For experimentalists, glyph-remote provides a separation of tasks: a ZeroMQ interface splits the genetic programming optimization task from the evaluation of an experimental (or numerical) run. Glyph can be accessed at http://github.com/ambrosys/glyph . Domain experts are be able to employ symbolic regression in their experiments with ease, even if they are not expert programmers. The reuse potential is kept high by a generic interface design. Glyph is available on PyPI and Github.

Learning Optimal Control of Synchronization in Networks of Coupled Oscillators using Genetic Programming-based Symbolic Regression

Networks of coupled dynamical systems provide a powerful way to model systems with enormously complex dynamics, such as the human brain. Control of synchronization in such networked systems has far reaching applications in many domains, including engineering and medicine. In this paper, we formulate the synchronization control in dynamical systems as an optimization problem and present a multi-objective genetic programming-based approach to infer optimal control functions that drive the system from a synchronized to a non-synchronized state and vice-versa. The genetic programming-based controller allows learning optimal control functions in an interpretable symbolic form. The effectiveness of the proposed approach is demonstrated in controlling synchronization in coupled oscillator systems linked in networks of increasing order complexity, ranging from a simple coupled oscillator system to a hierarchical network of coupled oscillators. The results show that the proposed method can learn highly-effective and interpretable control functions for such systems.