Combining Monte Carlo Tree Search and Heuristic Search for Weighted Vertex Coloring

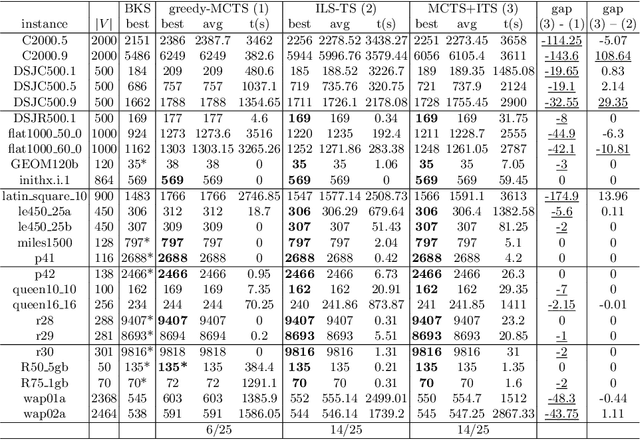
This work investigates the Monte Carlo Tree Search (MCTS) method combined with dedicated heuristics for solving the Weighted Vertex Coloring Problem. In addition to the basic MCTS algorithm, we study several MCTS variants where the conventional random simulation is replaced by other simulation strategies including greedy and local search heuristics. We conduct experiments on well-known benchmark instances to assess these combined MCTS variants. We provide empirical evidence to shed light on the advantages and limits of each simulation strategy. This is an extension of the work of Grelier and al. presented at EvoCOP2022.

On Monte Carlo Tree Search for Weighted Vertex Coloring

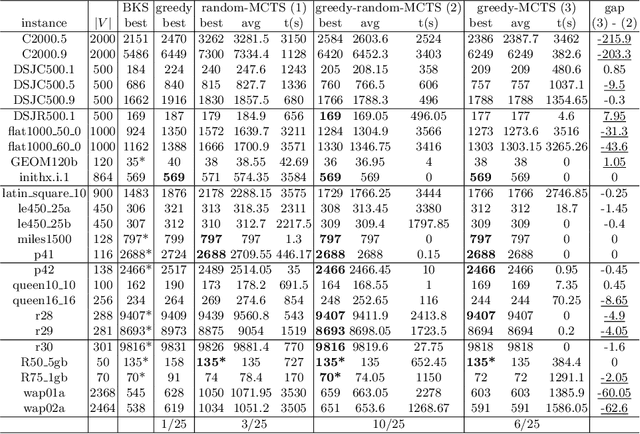
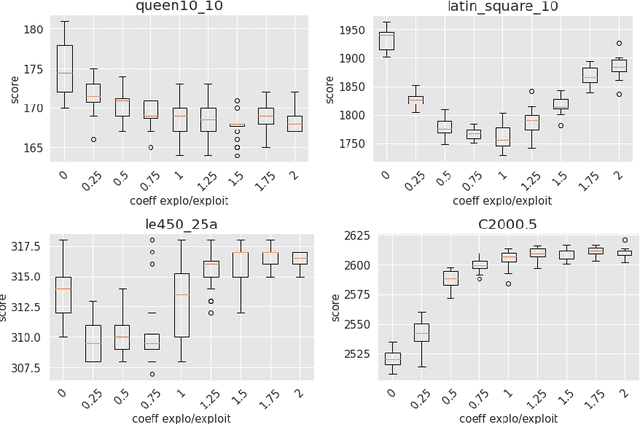
This work presents the first study of using the popular Monte Carlo Tree Search (MCTS) method combined with dedicated heuristics for solving the Weighted Vertex Coloring Problem. Starting with the basic MCTS algorithm, we gradually introduce a number of algorithmic variants where MCTS is extended by various simulation strategies including greedy and local search heuristics. We conduct experiments on well-known benchmark instances to assess the value of each studied combination. We also provide empirical evidence to shed light on the advantages and limits of each strategy.

A deep learning guided memetic framework for graph coloring problems

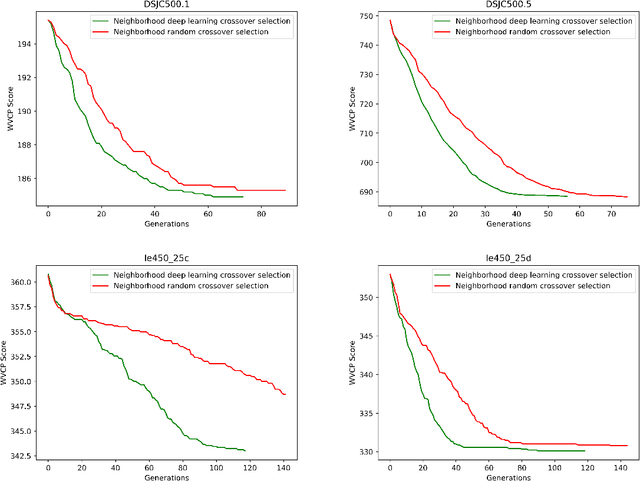
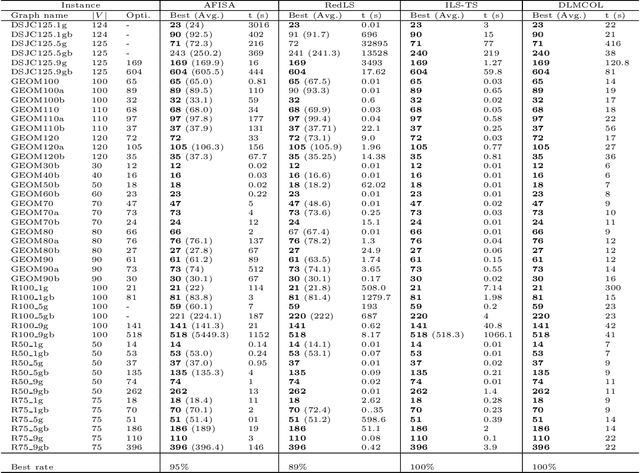
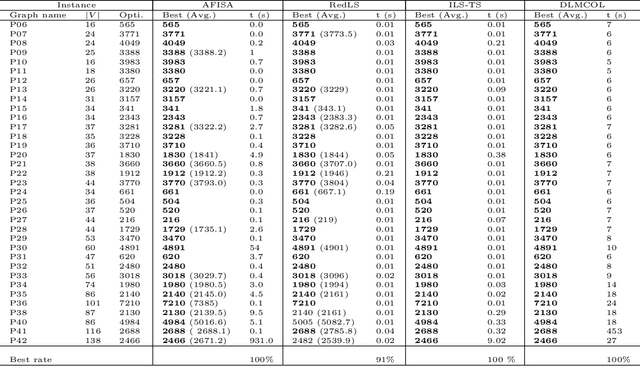
Given an undirected graph $G=(V,E)$ with a set of vertices $V$ and a set of edges $E$, a graph coloring problem involves finding a partition of the vertices into different independent sets. In this paper we present a new framework which combines a deep neural network with the best tools of "classical" metaheuristics for graph coloring. The proposed algorithm is evaluated on the weighted graph coloring problem and computational results show that the proposed approach allows to obtain new upper bounds for medium and large graphs. A study of the contribution of deep learning in the algorithm highlights that it is possible to learn relevant patterns useful to obtain better solutions to this problem.