Oleksandr Tkachenko
ScionFL: Secure Quantized Aggregation for Federated Learning
Oct 13, 2022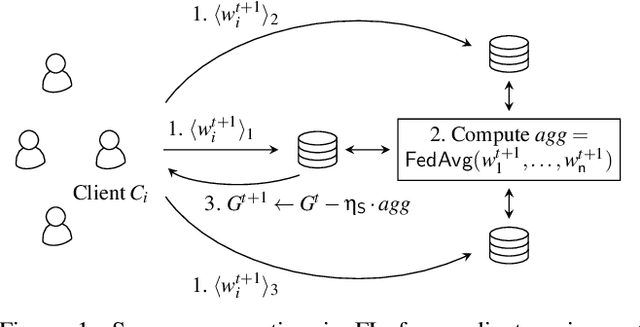
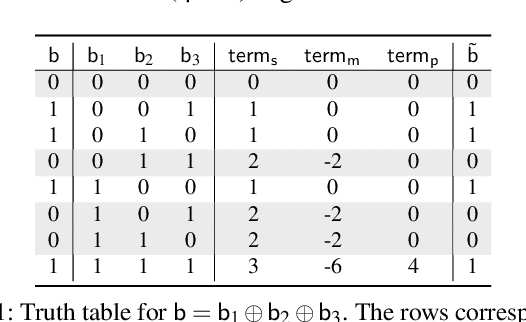

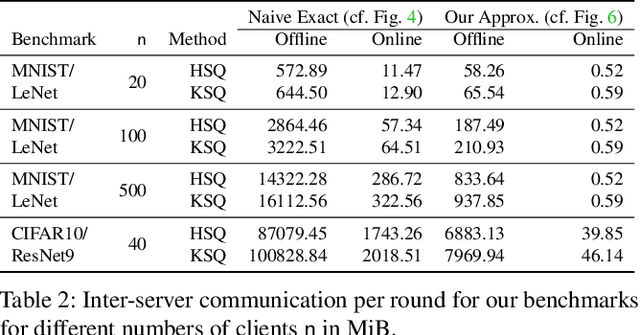
Abstract:Privacy concerns in federated learning (FL) are commonly addressed with secure aggregation schemes that prevent a central party from observing plaintext client updates. However, most such schemes neglect orthogonal FL research that aims at reducing communication between clients and the aggregator and is instrumental in facilitating cross-device FL with thousands and even millions of (mobile) participants. In particular, quantization techniques can typically reduce client-server communication by a factor of 32x. In this paper, we unite both research directions by introducing an efficient secure aggregation framework based on outsourced multi-party computation (MPC) that supports any linear quantization scheme. Specifically, we design a novel approximate version of an MPC-based secure aggregation protocol with support for multiple stochastic quantization schemes, including ones that utilize the randomized Hadamard transform and Kashin's representation. In our empirical performance evaluation, we show that with no additional overhead for clients and moderate inter-server communication, we achieve similar training accuracy as insecure schemes for standard FL benchmarks. Beyond this, we present an efficient extension to our secure quantized aggregation framework that effectively defends against state-of-the-art untargeted poisoning attacks.
Chameleon: A Hybrid Secure Computation Framework for Machine Learning Applications
Jan 10, 2018
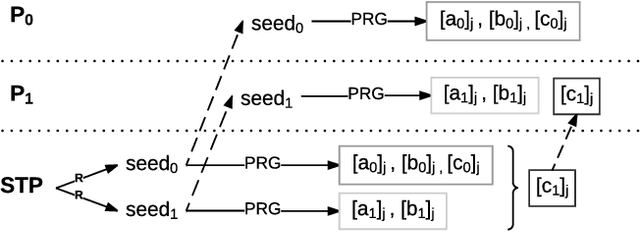


Abstract:We present Chameleon, a novel hybrid (mixed-protocol) framework for secure function evaluation (SFE) which enables two parties to jointly compute a function without disclosing their private inputs. Chameleon combines the best aspects of generic SFE protocols with the ones that are based upon additive secret sharing. In particular, the framework performs linear operations in the ring $\mathbb{Z}_{2^l}$ using additively secret shared values and nonlinear operations using Yao's Garbled Circuits or the Goldreich-Micali-Wigderson protocol. Chameleon departs from the common assumption of additive or linear secret sharing models where three or more parties need to communicate in the online phase: the framework allows two parties with private inputs to communicate in the online phase under the assumption of a third node generating correlated randomness in an offline phase. Almost all of the heavy cryptographic operations are precomputed in an offline phase which substantially reduces the communication overhead. Chameleon is both scalable and significantly more efficient than the ABY framework (NDSS'15) it is based on. Our framework supports signed fixed-point numbers. In particular, Chameleon's vector dot product of signed fixed-point numbers improves the efficiency of mining and classification of encrypted data for algorithms based upon heavy matrix multiplications. Our evaluation of Chameleon on a 5 layer convolutional deep neural network shows 133x and 4.2x faster executions than Microsoft CryptoNets (ICML'16) and MiniONN (CCS'17), respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge