Seq2Seq Models Reconstruct Visual Jigsaw Puzzles without Seeing Them

Jigsaw puzzles are primarily visual objects, whose algorithmic solutions have traditionally been framed from a visual perspective. In this work, however, we explore a fundamentally different approach: solving square jigsaw puzzles using language models, without access to raw visual input. By introducing a specialized tokenizer that converts each puzzle piece into a discrete sequence of tokens, we reframe puzzle reassembly as a sequence-to-sequence prediction task. Treated as "blind" solvers, encoder-decoder transformers accurately reconstruct the original layout by reasoning over token sequences alone. Despite being deliberately restricted from accessing visual input, our models achieve state-of-the-art results across multiple benchmarks, often outperforming vision-based methods. These findings highlight the surprising capability of language models to solve problems beyond their native domain, and suggest that unconventional approaches can inspire promising directions for puzzle-solving research.

Solving Convex Partition Visual Jigsaw Puzzles

Jigsaw puzzle solving requires the rearrangement of unordered pieces into their original pose in order to reconstruct a coherent whole, often an image, and is known to be an intractable problem. While the possible impact of automatic puzzle solvers can be disruptive in various application domains, most of the literature has focused on developing solvers for square jigsaw puzzles, severely limiting their practical use. In this work, we significantly expand the types of puzzles handled computationally, focusing on what is known as Convex Partitions, a major subset of polygonal puzzles whose pieces are convex. We utilize both geometrical and pictorial compatibilities, introduce a greedy solver, and report several performance measures next to the first benchmark dataset of such puzzles.

Recognizing Artistic Style of Archaeological Image Fragments Using Deep Style Extrapolation

Ancient artworks obtained in archaeological excavations usually suffer from a certain degree of fragmentation and physical degradation. Often, fragments of multiple artifacts from different periods or artistic styles could be found on the same site. With each fragment containing only partial information about its source, and pieces from different objects being mixed, categorizing broken artifacts based on their visual cues could be a challenging task, even for professionals. As classification is a common function of many machine learning models, the power of modern architectures can be harnessed for efficient and accurate fragment classification. In this work, we present a generalized deep-learning framework for predicting the artistic style of image fragments, achieving state-of-the-art results for pieces with varying styles and geometries.

Re-assembling the past: The RePAIR dataset and benchmark for real world 2D and 3D puzzle solving

This paper proposes the RePAIR dataset that represents a challenging benchmark to test modern computational and data driven methods for puzzle-solving and reassembly tasks. Our dataset has unique properties that are uncommon to current benchmarks for 2D and 3D puzzle solving. The fragments and fractures are realistic, caused by a collapse of a fresco during a World War II bombing at the Pompeii archaeological park. The fragments are also eroded and have missing pieces with irregular shapes and different dimensions, challenging further the reassembly algorithms. The dataset is multi-modal providing high resolution images with characteristic pictorial elements, detailed 3D scans of the fragments and meta-data annotated by the archaeologists. Ground truth has been generated through several years of unceasing fieldwork, including the excavation and cleaning of each fragment, followed by manual puzzle solving by archaeologists of a subset of approx. 1000 pieces among the 16000 available. After digitizing all the fragments in 3D, a benchmark was prepared to challenge current reassembly and puzzle-solving methods that often solve more simplistic synthetic scenarios. The tested baselines show that there clearly exists a gap to fill in solving this computationally complex problem.

Multi-Phase Relaxation Labeling for Square Jigsaw Puzzle Solving

We present a novel method for solving square jigsaw puzzles based on global optimization. The method is fully automatic, assumes no prior information, and can handle puzzles with known or unknown piece orientation. At the core of the optimization process is nonlinear relaxation labeling, a well-founded approach for deducing global solutions from local constraints, but unlike the classical scheme here we propose a multi-phase approach that guarantees convergence to feasible puzzle solutions. Next to the algorithmic novelty, we also present a new compatibility function for the quantification of the affinity between adjacent puzzle pieces. Competitive results and the advantage of the multi-phase approach are demonstrated on standard datasets.

Lazy caterer jigsaw puzzles: Models, properties, and a mechanical system-based solver

Jigsaw puzzle solving, the problem of constructing a coherent whole from a set of non-overlapping unordered fragments, is fundamental to numerous applications, and yet most of the literature has focused thus far on less realistic puzzles whose pieces are identical squares. Here we formalize a new type of jigsaw puzzle where the pieces are general convex polygons generated by cutting through a global polygonal shape with an arbitrary number of straight cuts, a generation model inspired by the celebrated Lazy caterer's sequence. We analyze the theoretical properties of such puzzles, including the inherent challenges in solving them once pieces are contaminated with geometrical noise. To cope with such difficulties and obtain tractable solutions, we abstract the problem as a multi-body spring-mass dynamical system endowed with hierarchical loop constraints and a layered reconstruction process. We define evaluation metrics and present experimental results to indicate that such puzzles are solvable completely automatically.

NTIRE 2020 Challenge on Spectral Reconstruction from an RGB Image

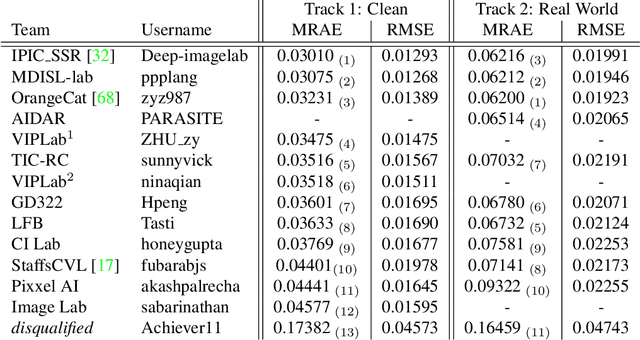
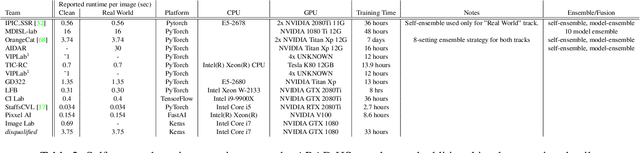
This paper reviews the second challenge on spectral reconstruction from RGB images, i.e., the recovery of whole-scene hyperspectral (HS) information from a 3-channel RGB image. As in the previous challenge, two tracks were provided: (i) a "Clean" track where HS images are estimated from noise-free RGBs, the RGB images are themselves calculated numerically using the ground-truth HS images and supplied spectral sensitivity functions (ii) a "Real World" track, simulating capture by an uncalibrated and unknown camera, where the HS images are recovered from noisy JPEG-compressed RGB images. A new, larger-than-ever, natural hyperspectral image data set is presented, containing a total of 510 HS images. The Clean and Real World tracks had 103 and 78 registered participants respectively, with 14 teams competing in the final testing phase. A description of the proposed methods, alongside their challenge scores and an extensive evaluation of top performing methods is also provided. They gauge the state-of-the-art in spectral reconstruction from an RGB image.

Contextual Object Detection with a Few Relevant Neighbors

A natural way to improve the detection of objects is to consider the contextual constraints imposed by the detection of additional objects in a given scene. In this work, we exploit the spatial relations between objects in order to improve detection capacity, as well as analyze various properties of the contextual object detection problem. To precisely calculate context-based probabilities of objects, we developed a model that examines the interactions between objects in an exact probabilistic setting, in contrast to previous methods that typically utilize approximations based on pairwise interactions. Such a scheme is facilitated by the realistic assumption that the existence of an object in any given location is influenced by only few informative locations in space. Based on this assumption, we suggest a method for identifying these relevant locations and integrating them into a mostly exact calculation of probability based on their raw detector responses. This scheme is shown to improve detection results and provides unique insights about the process of contextual inference for object detection. We show that it is generally difficult to learn that a particular object reduces the probability of another, and that in cases when the context and detector strongly disagree this learning becomes virtually impossible for the purposes of improving the results of an object detector. Finally, we demonstrate improved detection results through use of our approach as applied to the PASCAL VOC and COCO datasets.

Curve Reconstruction via the Global Statistics of Natural Curves

Reconstructing the missing parts of a curve has been the subject of much computational research, with applications in image inpainting, object synthesis, etc. Different approaches for solving that problem are typically based on processes that seek visually pleasing or perceptually plausible completions. In this work we focus on reconstructing the underlying physically likely shape by utilizing the global statistics of natural curves. More specifically, we develop a reconstruction model that seeks the mean physical curve for a given inducer configuration. This simple model is both straightforward to compute and it is receptive to diverse additional information, but it requires enough samples for all curve configurations, a practical requirement that limits its effective utilization. To address this practical issue we explore and exploit statistical geometrical properties of natural curves, and in particular, we show that in many cases the mean curve is scale invariant and oftentimes it is extensible. This, in turn, allows to boost the number of examples and thus the robustness of the statistics and its applicability. The reconstruction results are not only more physically plausible but they also lead to important insights on the reconstruction problem, including an elegant explanation why certain inducer configurations are more likely to yield consistent perceptual completions than others.

On the Utility of Context for Object Detection

The recurring context in which objects appear holds valuable information that can be employed to predict their existence. This intuitive observation indeed led many researchers to endow appearance-based detectors with explicit reasoning about context. The underlying thesis suggests that with stronger contextual relations, the better improvement in detection capacity one can expect from such a combined approach. In practice, however, the observed improvement in many case is modest at best, and often only marginal. In this work we seek to understand this phenomenon better, in part by pursuing an opposite approach. Instead of going from context to detection score, we formulate the score as a function of standard detector results and contextual relations, an approach that allows to treat the utility of context as an optimization problem in order to obtain the largest gain possible from considering context in the first place. Analyzing different contextual relations reveals the most helpful ones and shows that in many cases including context can help while in other cases a significant improvement is simply impossible or impractical. To better understand these results we then analyze the ability of context to handle different types of false detections, revealing that contextual information cannot ameliorate localization errors, which in turn also diminish the observed improvement obtained by correcting other types of errors. These insights provide further explanations and better understanding regarding the success or failure of utilizing context for object detection.