MindShift: Leveraging Large Language Models for Mental-States-Based Problematic Smartphone Use Intervention

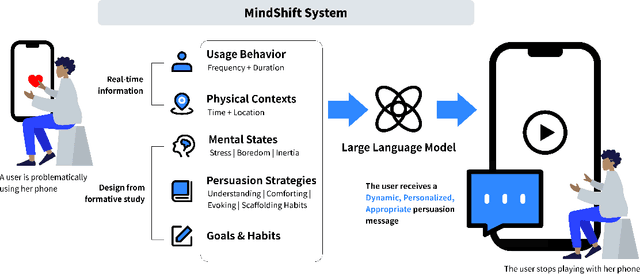
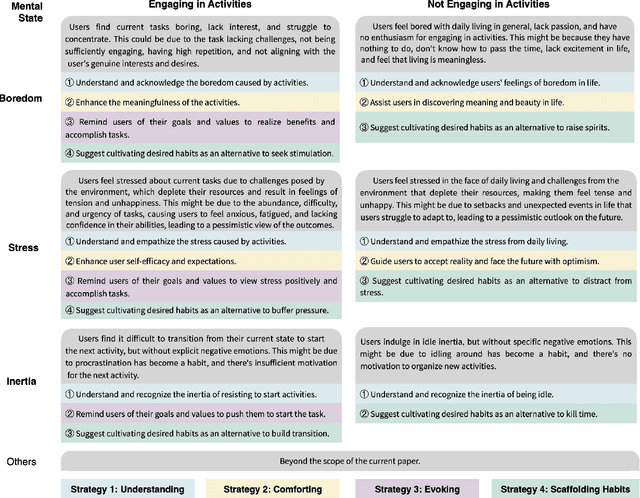
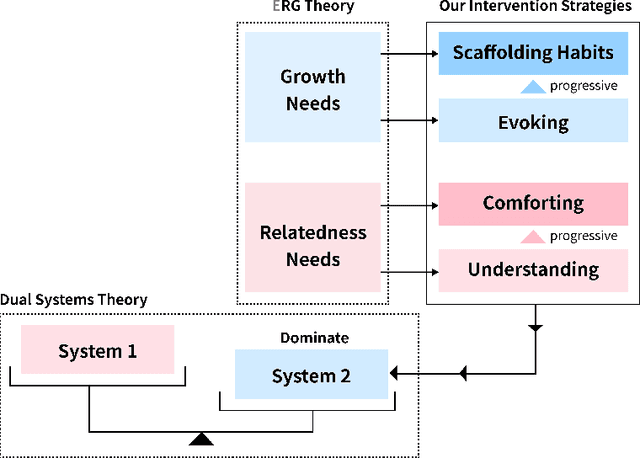
Problematic smartphone use negatively affects physical and mental health. Despite the wide range of prior research, existing persuasive techniques are not flexible enough to provide dynamic persuasion content based on users' physical contexts and mental states. We first conduct a Wizard-of-Oz study (N=12) and an interview study (N=10) to summarize the mental states behind problematic smartphone use: boredom, stress, and inertia. This informs our design of four persuasion strategies: understanding, comforting, evoking, and scaffolding habits. We leverage large language models (LLMs) to enable the automatic and dynamic generation of effective persuasion content. We develop MindShift, a novel LLM-powered problematic smartphone use intervention technique. MindShift takes users' in-the-moment physical contexts, mental states, app usage behaviors, users' goals & habits as input, and generates high-quality and flexible persuasive content with appropriate persuasion strategies. We conduct a 5-week field experiment (N=25) to compare MindShift with baseline techniques. The results show that MindShift significantly improves intervention acceptance rates by 17.8-22.5% and reduces smartphone use frequency by 12.1-14.4%. Moreover, users have a significant drop in smartphone addiction scale scores and a rise in self-efficacy. Our study sheds light on the potential of leveraging LLMs for context-aware persuasion in other behavior change domains.

Big portfolio selection by graph-based conditional moments method

How to do big portfolio selection is very important but challenging for both researchers and practitioners. In this paper, we propose a new graph-based conditional moments (GRACE) method to do portfolio selection based on thousands of stocks or more. The GRACE method first learns the conditional quantiles and mean of stock returns via a factor-augmented temporal graph convolutional network, which guides the learning procedure through a factor-hypergraph built by the set of stock-to-stock relations from the domain knowledge as well as the set of factor-to-stock relations from the asset pricing knowledge. Next, the GRACE method learns the conditional variance, skewness, and kurtosis of stock returns from the learned conditional quantiles by using the quantiled conditional moment (QCM) method. The QCM method is a supervised learning procedure to learn these conditional higher-order moments, so it largely overcomes the computational difficulty from the classical high-dimensional GARCH-type methods. Moreover, the QCM method allows the mis-specification in modeling conditional quantiles to some extent, due to its regression-based nature. Finally, the GRACE method uses the learned conditional mean, variance, skewness, and kurtosis to construct several performance measures, which are criteria to sort the stocks to proceed the portfolio selection in the well-known 10-decile framework. An application to NASDAQ and NYSE stock markets shows that the GRACE method performs much better than its competitors, particularly when the performance measures are comprised of conditional variance, skewness, and kurtosis.

Multiscale reconstruction of porous media based on multiple dictionaries learning

Digital modeling of the microstructure is important for studying the physical and transport properties of porous media. Multiscale modeling for porous media can accurately characterize macro-pores and micro-pores in a large-FoV (field of view) high-resolution three-dimensional pore structure model. This paper proposes a multiscale reconstruction algorithm based on multiple dictionaries learning, in which edge patterns and micro-pore patterns from homology high-resolution pore structure are introduced into low-resolution pore structure to build a fine multiscale pore structure model. The qualitative and quantitative comparisons of the experimental results show that the results of multiscale reconstruction are similar to the real high-resolution pore structure in terms of complex pore geometry and pore surface morphology. The geometric, topological and permeability properties of multiscale reconstruction results are almost identical to those of the real high-resolution pore structures. The experiments also demonstrate the proposal algorithm is capable of multiscale reconstruction without regard to the size of the input. This work provides an effective method for fine multiscale modeling of porous media.