PAITS: Pretraining and Augmentation for Irregularly-Sampled Time Series

Real-world time series data that commonly reflect sequential human behavior are often uniquely irregularly sampled and sparse, with highly nonuniform sampling over time and entities. Yet, commonly-used pretraining and augmentation methods for time series are not specifically designed for such scenarios. In this paper, we present PAITS (Pretraining and Augmentation for Irregularly-sampled Time Series), a framework for identifying suitable pretraining strategies for sparse and irregularly sampled time series datasets. PAITS leverages a novel combination of NLP-inspired pretraining tasks and augmentations, and a random search to identify an effective strategy for a given dataset. We demonstrate that different datasets benefit from different pretraining choices. Compared with prior methods, our approach is better able to consistently improve pretraining across multiple datasets and domains. Our code is available at \url{https://github.com/google-research/google-research/tree/master/irregular_timeseries_pretraining}.

Moment Matching Deep Contrastive Latent Variable Models

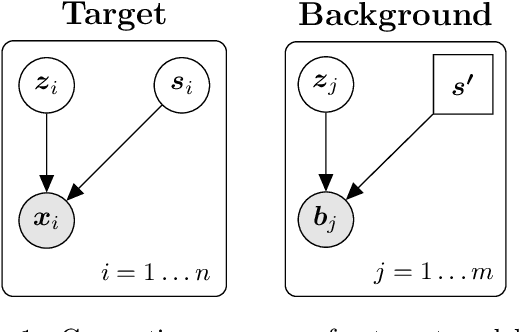
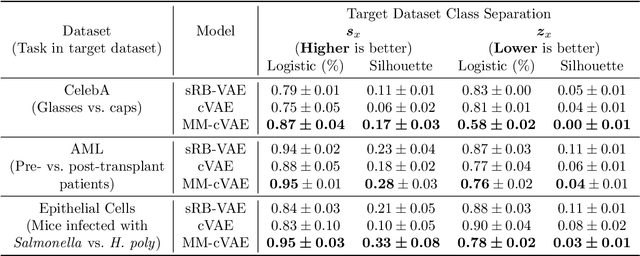
In the contrastive analysis (CA) setting, machine learning practitioners are specifically interested in discovering patterns that are enriched in a target dataset as compared to a background dataset generated from sources of variation irrelevant to the task at hand. For example, a biomedical data analyst may seek to understand variations in genomic data only present among patients with a given disease as opposed to those also present in healthy control subjects. Such scenarios have motivated the development of contrastive latent variable models to isolate variations unique to these target datasets from those shared across the target and background datasets, with current state of the art models based on the variational autoencoder (VAE) framework. However, previously proposed models do not explicitly enforce the constraints on latent variables underlying CA, potentially leading to the undesirable leakage of information between the two sets of latent variables. Here we propose the moment matching contrastive VAE (MM-cVAE), a reformulation of the VAE for CA that uses the maximum mean discrepancy to explicitly enforce two crucial latent variable constraints underlying CA. On three challenging CA tasks we find that our method outperforms the previous state-of-the-art both qualitatively and on a set of quantitative metrics.