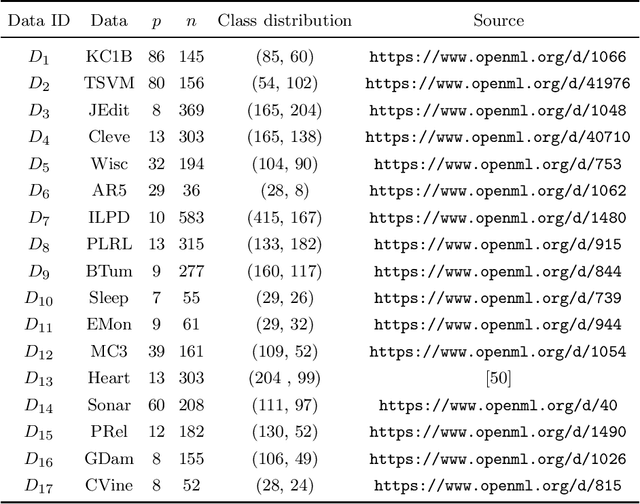
A k nearest neighbours classifiers ensemble based on extended neighbourhood rule and features subsets

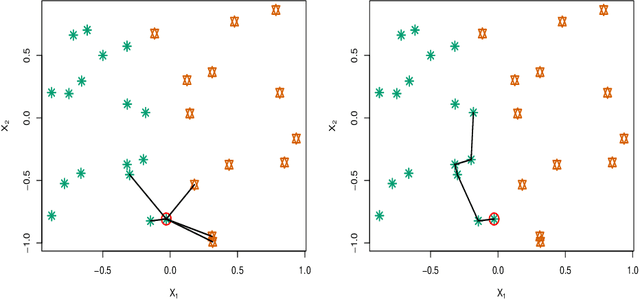
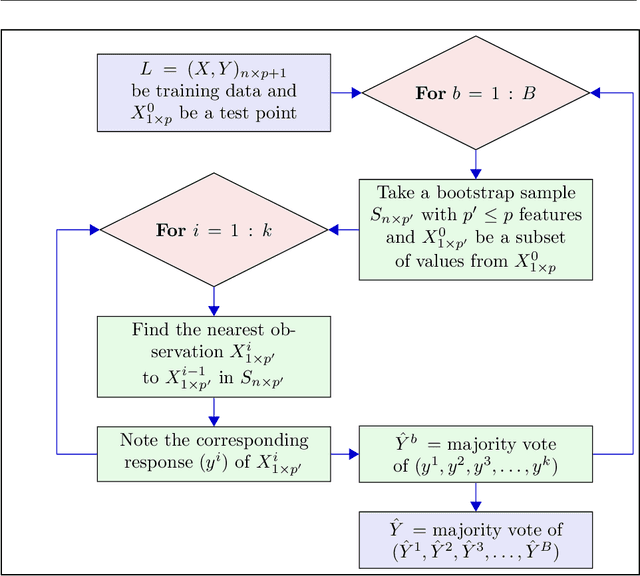
kNN based ensemble methods minimise the effect of outliers by identifying a set of data points in the given feature space that are nearest to an unseen observation in order to predict its response by using majority voting. The ordinary ensembles based on kNN find out the k nearest observations in a region (bounded by a sphere) based on a predefined value of k. This scenario, however, might not work in situations when the test observation follows the pattern of the closest data points with the same class that lie on a certain path not contained in the given sphere. This paper proposes a k nearest neighbour ensemble where the neighbours are determined in k steps. Starting from the first nearest observation of the test point, the algorithm identifies a single observation that is closest to the observation at the previous step. At each base learner in the ensemble, this search is extended to k steps on a random bootstrap sample with a random subset of features selected from the feature space. The final predicted class of the test point is determined by using a majority vote in the predicted classes given by all base models. This new ensemble method is applied on 17 benchmark datasets and compared with other classical methods, including kNN based models, in terms of classification accuracy, kappa and Brier score as performance metrics. Boxplots are also utilised to illustrate the difference in the results given by the proposed and other state-of-the-art methods. The proposed method outperformed the rest of the classical methods in the majority of cases. The paper gives a detailed simulation study for further assessment.

Optimal trees selection for classification via out-of-bag assessment and sub-bagging

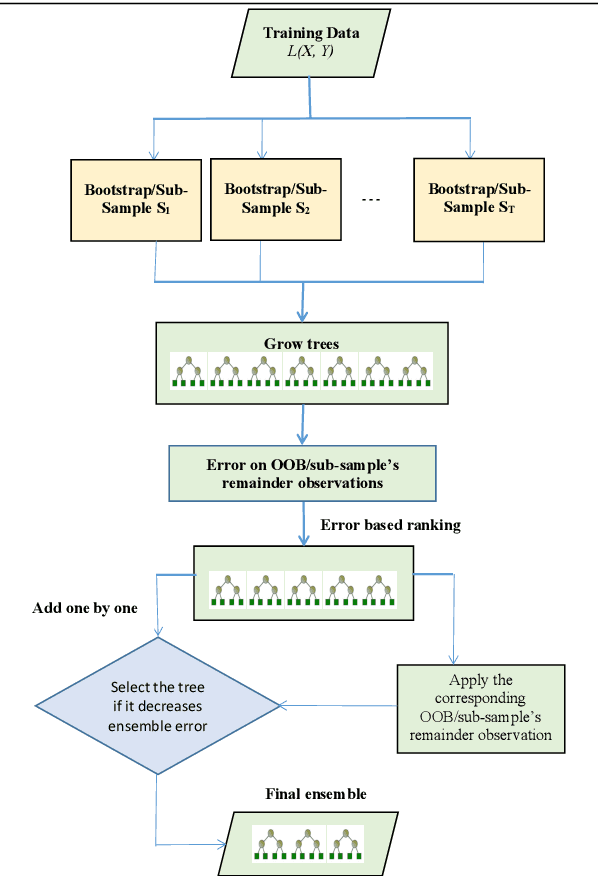
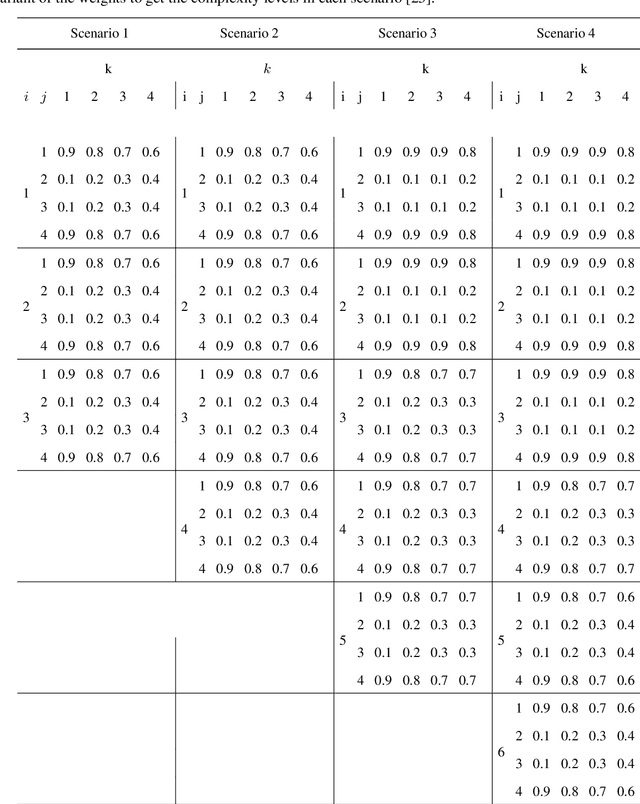
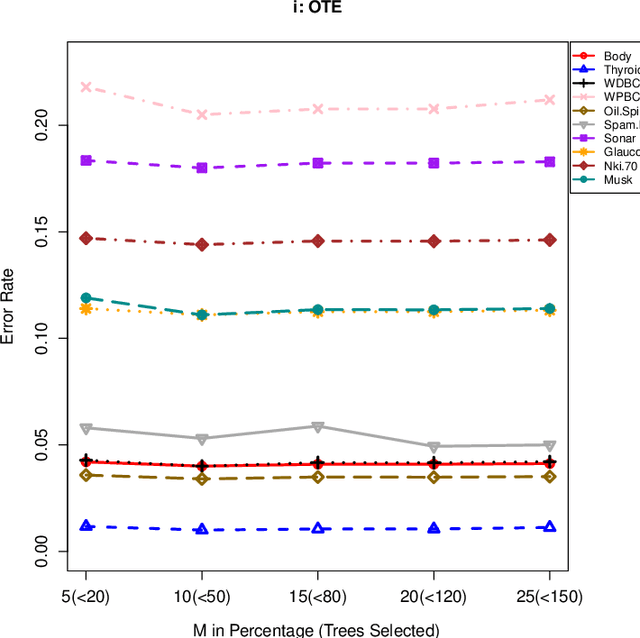
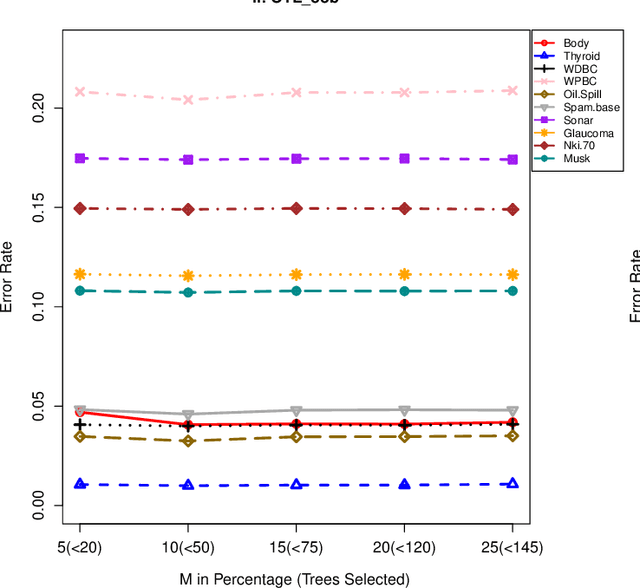
The effect of training data size on machine learning methods has been well investigated over the past two decades. The predictive performance of tree based machine learning methods, in general, improves with a decreasing rate as the size of training data increases. We investigate this in optimal trees ensemble (OTE) where the method fails to learn from some of the training observations due to internal validation. Modified tree selection methods are thus proposed for OTE to cater for the loss of training observations in internal validation. In the first method, corresponding out-of-bag (OOB) observations are used in both individual and collective performance assessment for each tree. Trees are ranked based on their individual performance on the OOB observations. A certain number of top ranked trees is selected and starting from the most accurate tree, subsequent trees are added one by one and their impact is recorded by using the OOB observations left out from the bootstrap sample taken for the tree being added. A tree is selected if it improves predictive accuracy of the ensemble. In the second approach, trees are grown on random subsets, taken without replacement-known as sub-bagging, of the training data instead of bootstrap samples (taken with replacement). The remaining observations from each sample are used in both individual and collective assessments for each corresponding tree similar to the first method. Analysis on 21 benchmark datasets and simulations studies show improved performance of the modified methods in comparison to OTE and other state-of-the-art methods.

Optimal survival trees ensemble

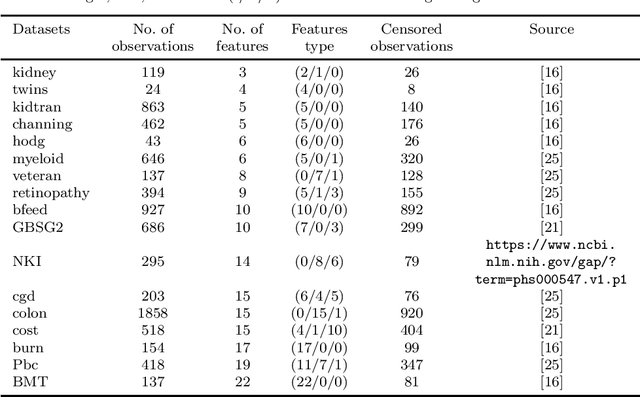
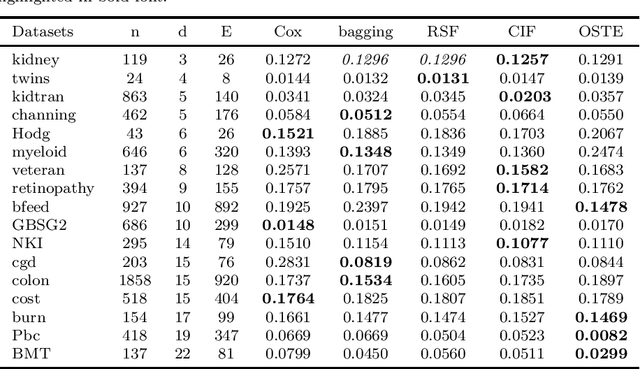
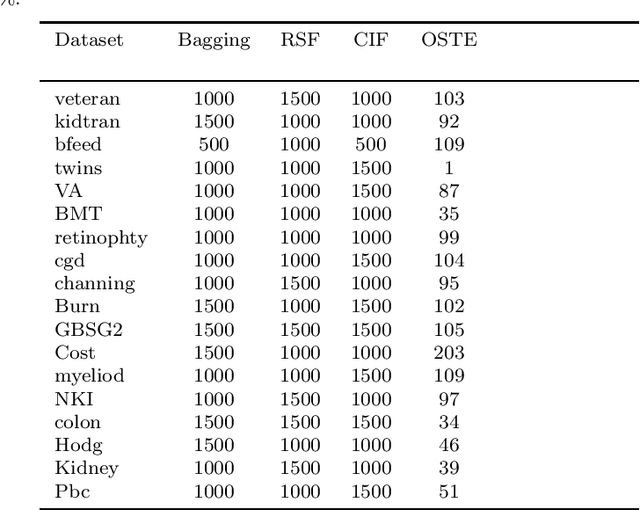
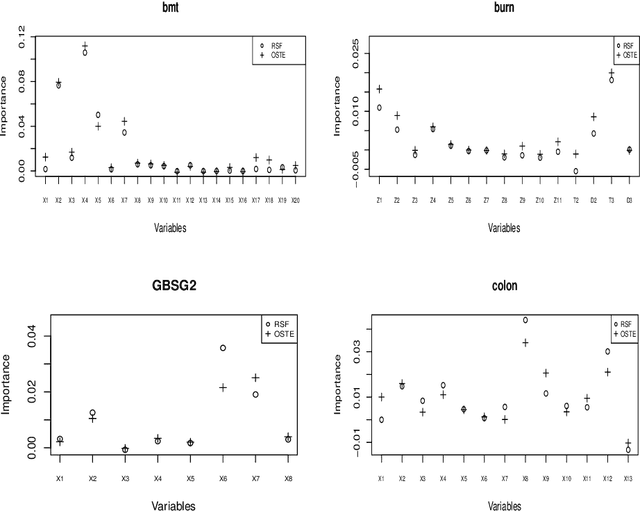
Recent studies have adopted an approach of selecting accurate and diverse trees based on individual or collective performance within an ensemble for classification and regression problems. This work follows in the wake of these investigations and considers the possibility of growing a forest of optimal survival trees. Initially, a large set of survival trees are grown using the method of random survival forest. The grown trees are then ranked from smallest to highest value of their prediction error using out-of-bag observations for each respective survival tree. The top ranked survival trees are then assessed for their collective performance as an ensemble. This ensemble is initiated with the survival tree which stands first in rank, then further trees are tested one by one by adding them to the ensemble in order of rank. A survival tree is selected for the resultant ensemble if the performance improves after an assessment using independent training data. This ensemble is called an optimal trees ensemble (OSTE). The proposed method is assessed using 17 benchmark datasets and the results are compared with those of random survival forest, conditional inference forest, bagging and a non tree based method, the Cox proportional hazard model. In addition to improve predictive performance, the proposed method reduces the number of survival trees in the ensemble as compared to the other tree based methods. The method is implemented in an R package called "OSTE".