A Random Projection k Nearest Neighbours Ensemble for Classification via Extended Neighbourhood Rule

Ensembles based on k nearest neighbours (kNN) combine a large number of base learners, each constructed on a sample taken from a given training data. Typical kNN based ensembles determine the k closest observations in the training data bounded to a test sample point by a spherical region to predict its class. In this paper, a novel random projection extended neighbourhood rule (RPExNRule) ensemble is proposed where bootstrap samples from the given training data are randomly projected into lower dimensions for additional randomness in the base models and to preserve features information. It uses the extended neighbourhood rule (ExNRule) to fit kNN as base learners on randomly projected bootstrap samples.

An Optimal k Nearest Neighbours Ensemble for Classification Based on Extended Neighbourhood Rule with Features subspace

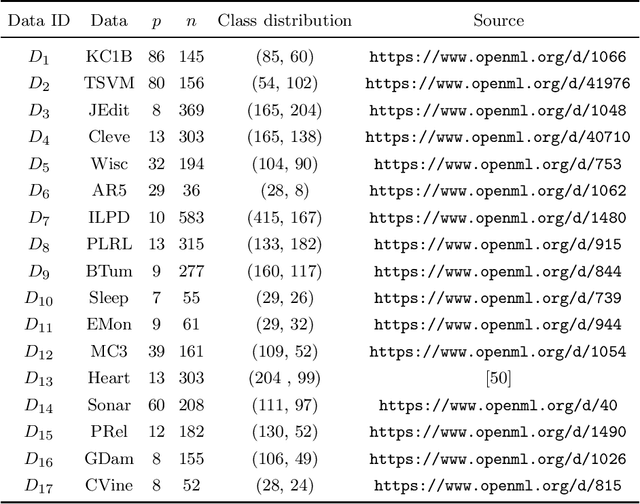
To minimize the effect of outliers, kNN ensembles identify a set of closest observations to a new sample point to estimate its unknown class by using majority voting in the labels of the training instances in the neighbourhood. Ordinary kNN based procedures determine k closest training observations in the neighbourhood region (enclosed by a sphere) by using a distance formula. The k nearest neighbours procedure may not work in a situation where sample points in the test data follow the pattern of the nearest observations that lie on a certain path not contained in the given sphere of nearest neighbours. Furthermore, these methods combine hundreds of base kNN learners and many of them might have high classification errors thereby resulting in poor ensembles. To overcome these problems, an optimal extended neighbourhood rule based ensemble is proposed where the neighbours are determined in k steps. It starts from the first nearest sample point to the unseen observation. The second nearest data point is identified that is closest to the previously selected data point. This process is continued until the required number of the k observations are obtained. Each base model in the ensemble is constructed on a bootstrap sample in conjunction with a random subset of features. After building a sufficiently large number of base models, the optimal models are then selected based on their performance on out-of-bag (OOB) data.

A k nearest neighbours classifiers ensemble based on extended neighbourhood rule and features subsets

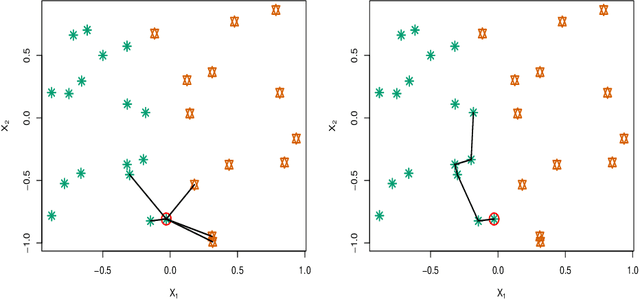
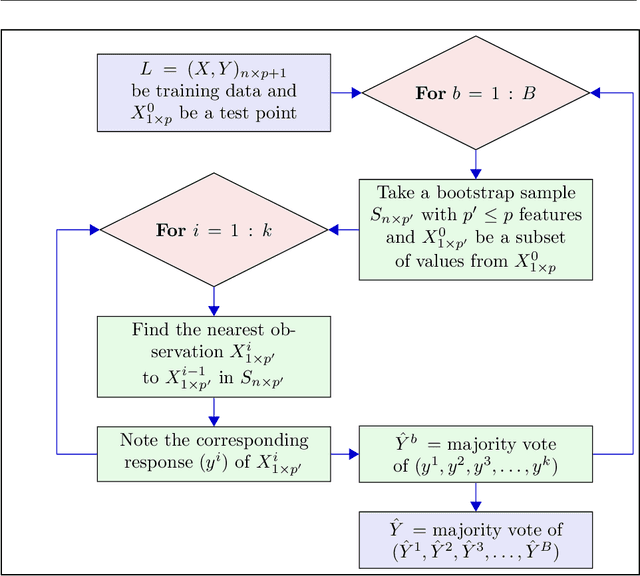
kNN based ensemble methods minimise the effect of outliers by identifying a set of data points in the given feature space that are nearest to an unseen observation in order to predict its response by using majority voting. The ordinary ensembles based on kNN find out the k nearest observations in a region (bounded by a sphere) based on a predefined value of k. This scenario, however, might not work in situations when the test observation follows the pattern of the closest data points with the same class that lie on a certain path not contained in the given sphere. This paper proposes a k nearest neighbour ensemble where the neighbours are determined in k steps. Starting from the first nearest observation of the test point, the algorithm identifies a single observation that is closest to the observation at the previous step. At each base learner in the ensemble, this search is extended to k steps on a random bootstrap sample with a random subset of features selected from the feature space. The final predicted class of the test point is determined by using a majority vote in the predicted classes given by all base models. This new ensemble method is applied on 17 benchmark datasets and compared with other classical methods, including kNN based models, in terms of classification accuracy, kappa and Brier score as performance metrics. Boxplots are also utilised to illustrate the difference in the results given by the proposed and other state-of-the-art methods. The proposed method outperformed the rest of the classical methods in the majority of cases. The paper gives a detailed simulation study for further assessment.