A Simple and Strong Baseline for End-to-End Neural RST-style Discourse Parsing

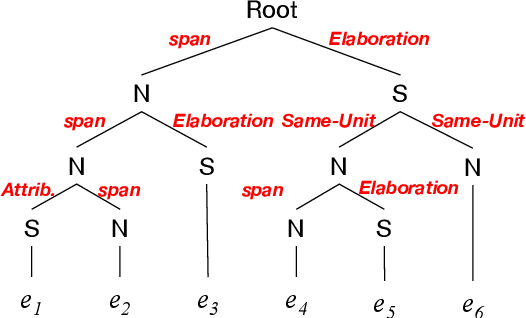
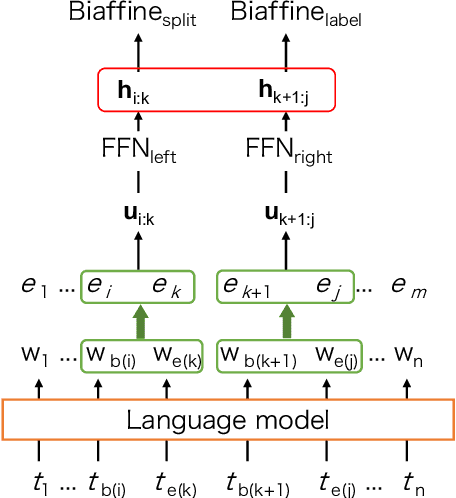
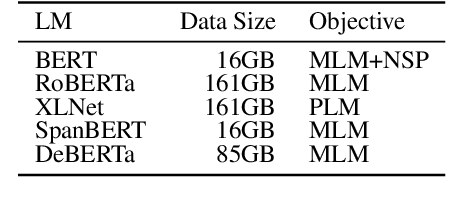
To promote and further develop RST-style discourse parsing models, we need a strong baseline that can be regarded as a reference for reporting reliable experimental results. This paper explores a strong baseline by integrating existing simple parsing strategies, top-down and bottom-up, with various transformer-based pre-trained language models. The experimental results obtained from two benchmark datasets demonstrate that the parsing performance strongly relies on the pretrained language models rather than the parsing strategies. In particular, the bottom-up parser achieves large performance gains compared to the current best parser when employing DeBERTa. We further reveal that language models with a span-masking scheme especially boost the parsing performance through our analysis within intra- and multi-sentential parsing, and nuclearity prediction.

Toward Neural-Network-Guided Program Synthesis and Verification

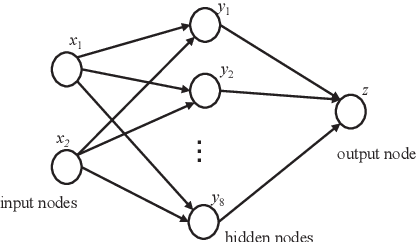
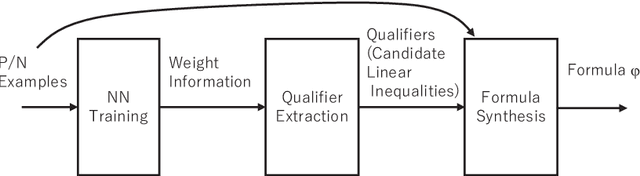
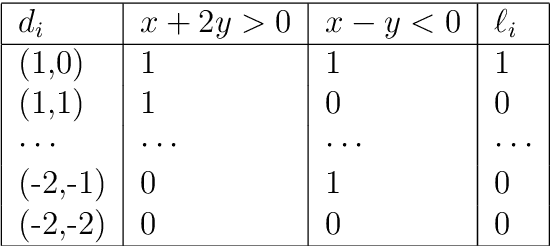
We propose a novel framework of program and invariant synthesis called neural network-guided synthesis. We first show that, by suitably designing and training neural networks, we can extract logical formulas over integers from the weights and biases of the trained neural networks. Based on the idea, we have implemented a tool to synthesize formulas from positive/negative examples and implication constraints, and obtained promising experimental results. We also discuss two applications of our synthesis method. One is the use of our tool for qualifier discovery in the framework of ICE-learning-based CHC solving, which can in turn be applied to program verification and inductive invariant synthesis. Another application is to a new program development framework called oracle-based programming, which is a neural-network-guided variation of Solar-Lezama's program synthesis by sketching.

A Cyclic Proof System for HFLN

A cyclic proof system allows us to perform inductive reasoning without explicit inductions. We propose a cyclic proof system for HFLN, which is a higher-order predicate logic with natural numbers and alternating fixed-points. Ours is the first cyclic proof system for a higher-order logic, to our knowledge. Due to the presence of higher-order predicates and alternating fixed-points, our cyclic proof system requires a more delicate global condition on cyclic proofs than the original system of Brotherston and Simpson. We prove the decidability of checking the global condition and soundness of this system, and also prove a restricted form of standard completeness for an infinitary variant of our cyclic proof system. A potential application of our cyclic proof system is semi-automated verification of higher-order programs, based on Kobayashi et al.'s recent work on reductions from program verification to HFLN validity checking.