Enhancing Loop-Invariant Synthesis via Reinforcement Learning

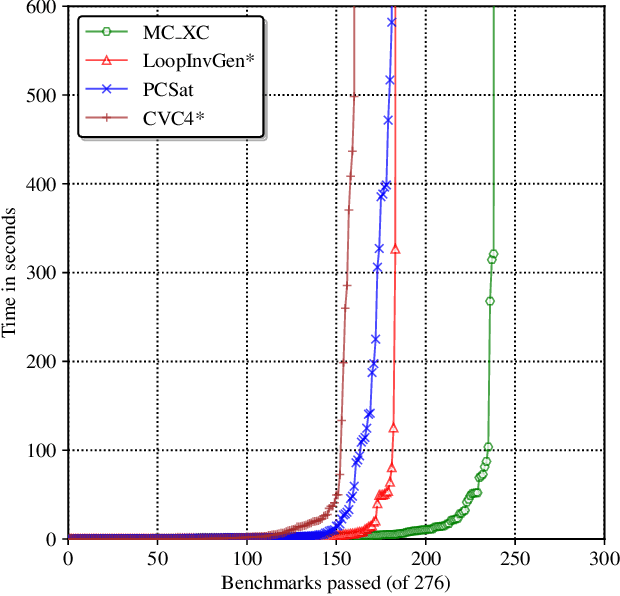
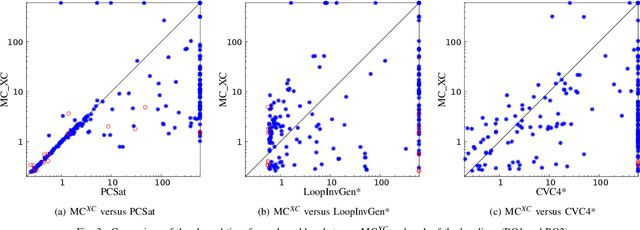
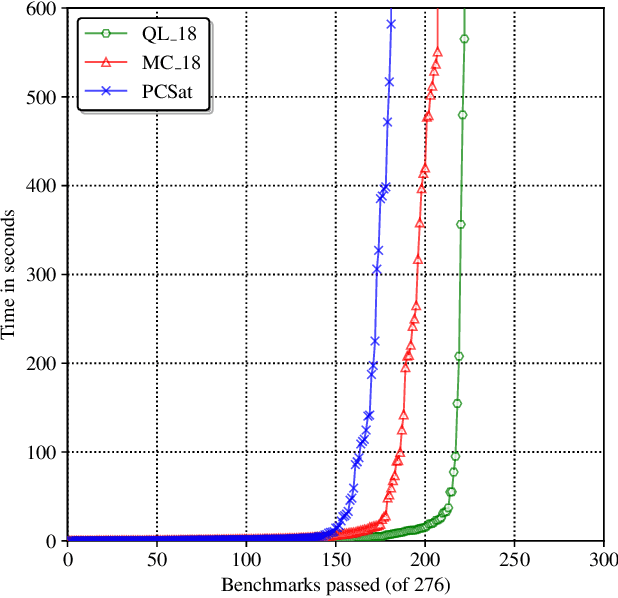
Loop-invariant synthesis is the basis of every program verification procedure. Due to its undecidability in general, a tool for invariant synthesis necessarily uses heuristics. Despite the common belief that the design of heuristics is vital for the effective performance of a verifier, little work has been performed toward obtaining the optimal heuristics for each invariant-synthesis tool. Instead, developers have hand-tuned the heuristics of tools. This study demonstrates that we can effectively and automatically learn a good heuristic via reinforcement learning for an invariant synthesizer PCSat. Our experiment shows that PCSat combined with the heuristic learned by reinforcement learning outperforms the state-of-the-art solvers for this task. To the best of our knowledge, this is the first work that investigates learning the heuristics of an invariant synthesis tool.

A Cyclic Proof System for HFLN

A cyclic proof system allows us to perform inductive reasoning without explicit inductions. We propose a cyclic proof system for HFLN, which is a higher-order predicate logic with natural numbers and alternating fixed-points. Ours is the first cyclic proof system for a higher-order logic, to our knowledge. Due to the presence of higher-order predicates and alternating fixed-points, our cyclic proof system requires a more delicate global condition on cyclic proofs than the original system of Brotherston and Simpson. We prove the decidability of checking the global condition and soundness of this system, and also prove a restricted form of standard completeness for an infinitary variant of our cyclic proof system. A potential application of our cyclic proof system is semi-automated verification of higher-order programs, based on Kobayashi et al.'s recent work on reductions from program verification to HFLN validity checking.