Generalized Gaussian Temporal Difference Error For Uncertainty-aware Reinforcement Learning

Conventional uncertainty-aware temporal difference (TD) learning methods often rely on simplistic assumptions, typically including a zero-mean Gaussian distribution for TD errors. Such oversimplification can lead to inaccurate error representations and compromised uncertainty estimation. In this paper, we introduce a novel framework for generalized Gaussian error modeling in deep reinforcement learning, applicable to both discrete and continuous control settings. Our framework enhances the flexibility of error distribution modeling by incorporating higher-order moments, particularly kurtosis, thereby improving the estimation and mitigation of data-dependent noise, i.e., aleatoric uncertainty. We examine the influence of the shape parameter of the generalized Gaussian distribution (GGD) on aleatoric uncertainty and provide a closed-form expression that demonstrates an inverse relationship between uncertainty and the shape parameter. Additionally, we propose a theoretically grounded weighting scheme to fully leverage the GGD. To address epistemic uncertainty, we enhance the batch inverse variance weighting by incorporating bias reduction and kurtosis considerations, resulting in improved robustness. Extensive experimental evaluations using policy gradient algorithms demonstrate the consistent efficacy of our method, showcasing significant performance improvements.

Synchronisation-Oriented Design Approach for Adaptive Control

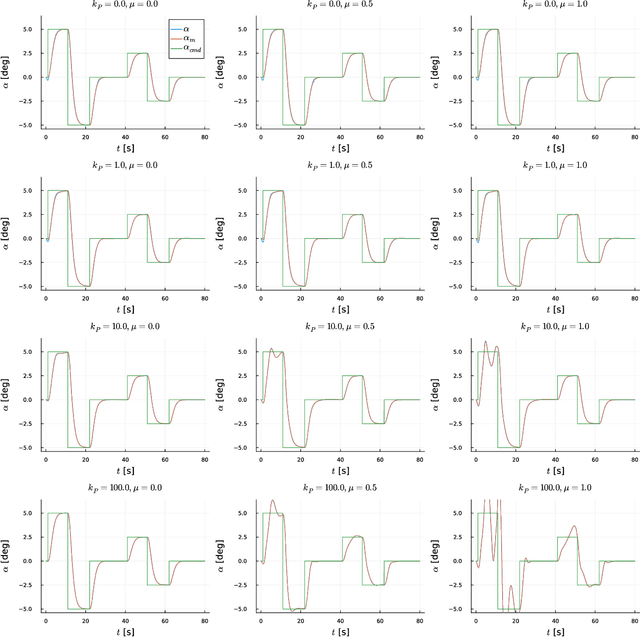
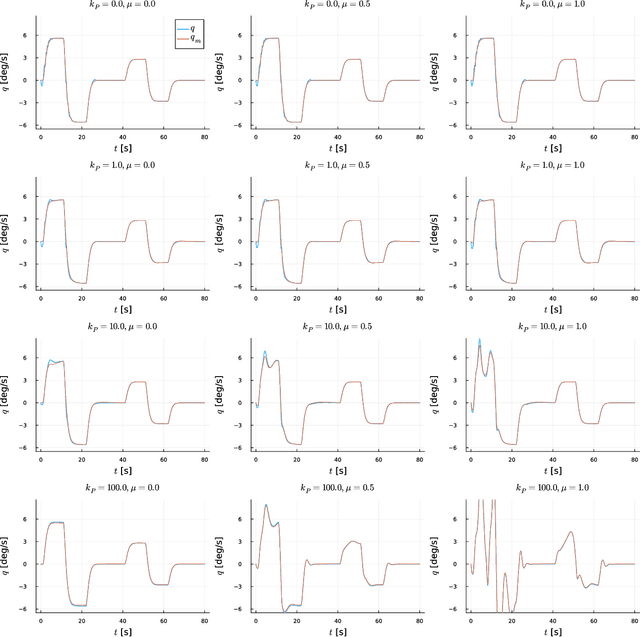
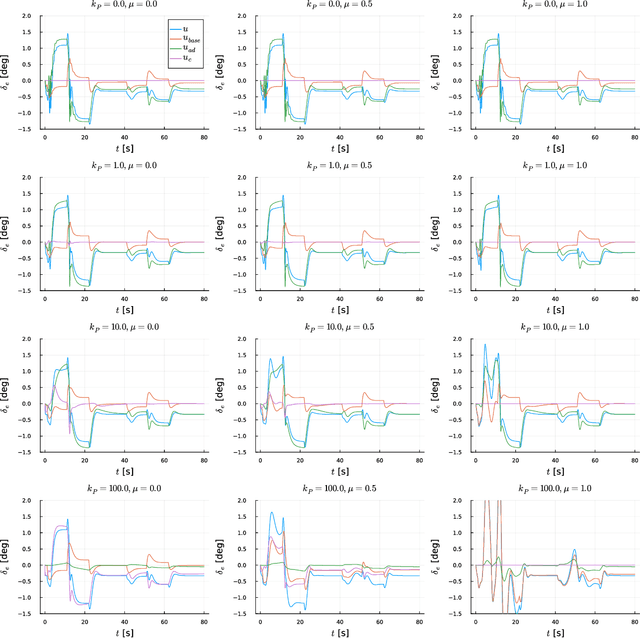
This study presents a synchronisation-oriented perspective towards adaptive control which views model-referenced adaptation as synchronisation between actual and virtual dynamic systems. In the context of adaptation, model reference adaptive control methods make the state response of the actual plant follow a reference model. In the context of synchronisation, consensus methods involving diffusive coupling induce a collective behaviour across multiple agents. We draw from the understanding about the two time-scale nature of synchronisation motivated by the study of blended dynamics. The synchronisation-oriented approach consists in the design of a coupling input to achieve desired closed-loop error dynamics followed by the input allocation process to shape the collective behaviour. We suggest that synchronisation can be a reasonable design principle allowing a more holistic and systematic approach to the design of adaptive control systems for improved transient characteristics. Most notably, the proposed approach enables not only constructive derivation but also substantial generalisation of the previously developed closed-loop reference model adaptive control method. Practical significance of the proposed generalisation lies at the capability to improve the transient response characteristics and mitigate the unwanted peaking phenomenon at the same time.

Automatic Optimisation of Normalised Neural Networks

We propose automatic optimisation methods considering the geometry of matrix manifold for the normalised parameters of neural networks. Layerwise weight normalisation with respect to Frobenius norm is utilised to bound the Lipschitz constant and to enhance gradient reliability so that the trained networks are suitable for control applications. Our approach first initialises the network and normalises the data with respect to the $\ell^{2}$-$\ell^{2}$ gain of the initialised network. Then, the proposed algorithms take the update structure based on the exponential map on high-dimensional spheres. Given an update direction such as that of the negative Riemannian gradient, we propose two different ways to determine the stepsize for descent. The first algorithm utilises automatic differentiation of the objective function along the update curve defined on the combined manifold of spheres. The directional second-order derivative information can be utilised without requiring explicit construction of the Hessian. The second algorithm utilises the majorisation-minimisation framework via architecture-aware majorisation for neural networks. With these new developments, the proposed methods avoid manual tuning and scheduling of the learning rate, thus providing an automated pipeline for optimizing normalised neural networks.

Dynamic deep-reinforcement-learning algorithm in Partially Observed Markov Decision Processes

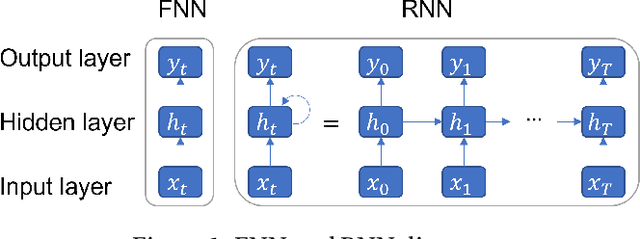
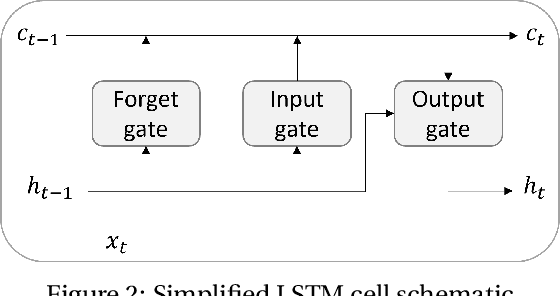
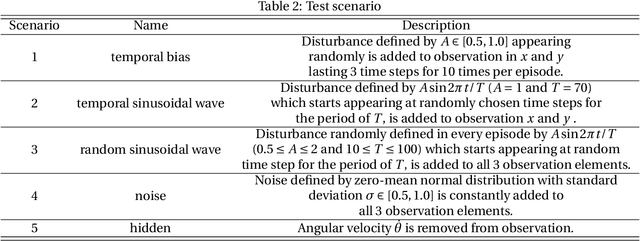
Reinforcement learning has been greatly improved in recent studies and an increased interest in real-world implementation has emerged in recent years. In many cases, due to the non-static disturbances, it becomes challenging for the agent to keep the performance. The disturbance results in the environment called Partially Observable Markov Decision Process. In common practice, Partially Observable Markov Decision Process is handled by introducing an additional estimator, or Recurrent Neural Network is utilized in the context of reinforcement learning. Both of the cases require to process sequential information on the trajectory. However, there are only a few studies investigating the effect of information to consider and the network structure to handle them. This study shows the benefit of action sequence inclusion in order to solve Partially Observable Markov Decision Process. Several structures and approaches are proposed to extend one of the latest deep reinforcement learning algorithms with LSTM networks. The developed algorithms showed enhanced robustness of controller performance against different types of external disturbances that are added to observation.

A Passivity-Based Method for Accelerated Convex Optimisation

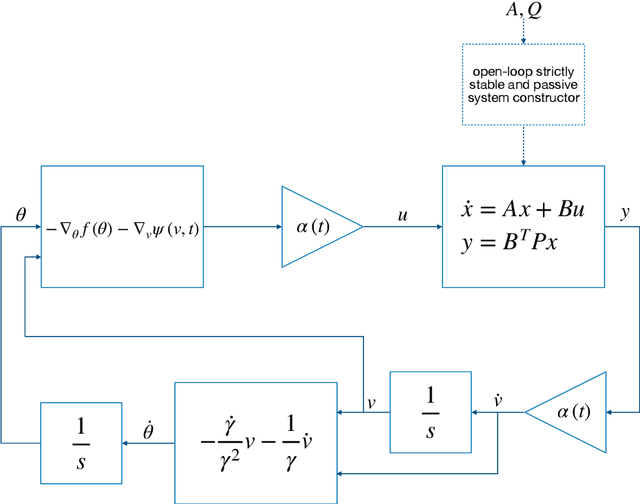
This study presents a constructive methodology for designing accelerated convex optimisation algorithms in continuous-time domain. The two key enablers are the classical concept of passivity in control theory and the time-dependent change of variables that maps the output of the internal dynamic system to the optimisation variables. The Lyapunov function associated with the optimisation dynamics is obtained as a natural consequence of specifying the internal dynamics that drives the state evolution as a passive linear time-invariant system. The passivity-based methodology provides a general framework that has the flexibility to generate convex optimisation algorithms with the guarantee of different convergence rate bounds on the objective function value. The same principle applies to the design of online parameter update algorithms for adaptive control by re-defining the output of internal dynamics to allow for the feedback interconnection with tracking error dynamics.

Incremental Correction in Dynamic Systems Modelled with Neural Networks for Constraint Satisfaction

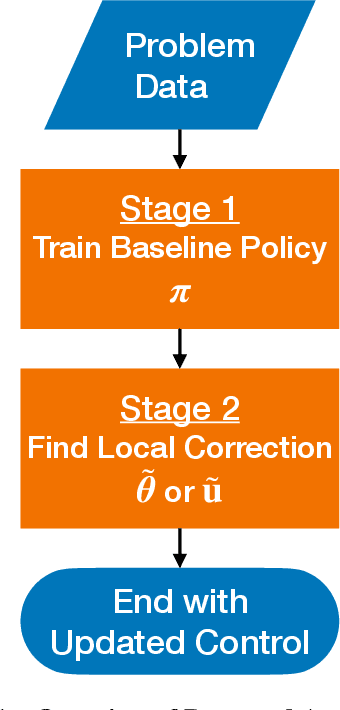
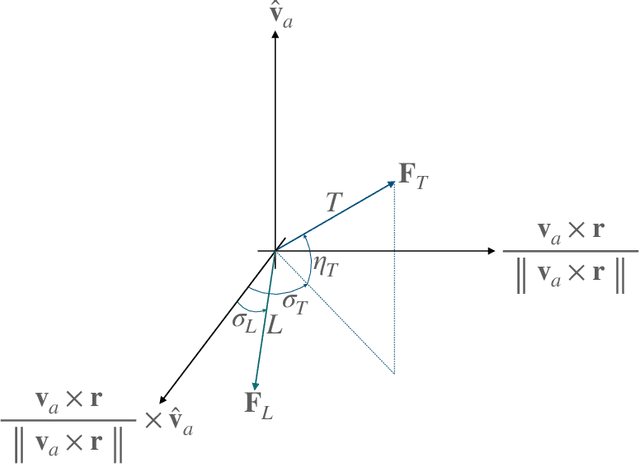
This study presents incremental correction methods for refining neural network parameters or control functions entering into a continuous-time dynamic system to achieve improved solution accuracy in satisfying the interim point constraints placed on the performance output variables. The proposed approach is to linearise the dynamics around the baseline values of its arguments, and then to solve for the corrective input required to transfer the perturbed trajectory to precisely known or desired values at specific time points, i.e., the interim points. Depending on the type of decision variables to adjust, parameter correction and control function correction methods are developed. These incremental correction methods can be utilised as a means to compensate for the prediction errors of pre-trained neural networks in real-time applications where high accuracy of the prediction of dynamical systems at prescribed time points is imperative. In this regard, the online update approach can be useful for enhancing overall targeting accuracy of finite-horizon control subject to point constraints using a neural policy. Numerical example demonstrates the effectiveness of the proposed approach in an application to a powered descent problem at Mars.

Bayesian Learning Approach to Model Predictive Control

This study presents a Bayesian learning perspective towards model predictive control algorithms. High-level frameworks have been developed separately in the earlier studies on Bayesian learning and sampling-based model predictive control. On one hand, the Bayesian learning rule provides a general framework capable of generating various machine learning algorithms as special instances. On the other hand, the dynamic mirror descent model predictive control framework is capable of diversifying sample-rollout-based control algorithms. However, connections between the two frameworks have still not been fully appreciated in the context of stochastic optimal control. This study combines the Bayesian learning rule point of view into the model predictive control setting by taking inspirations from the view of understanding model predictive controller as an online learner. The selection of posterior class and natural gradient approximation for the variational formulation governs diversification of model predictive control algorithms in the Bayesian learning approach to model predictive control. This alternative viewpoint complements the dynamic mirror descent framework through streamlining the explanation of design choices.

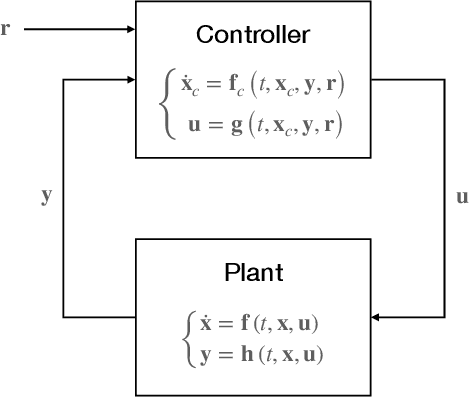
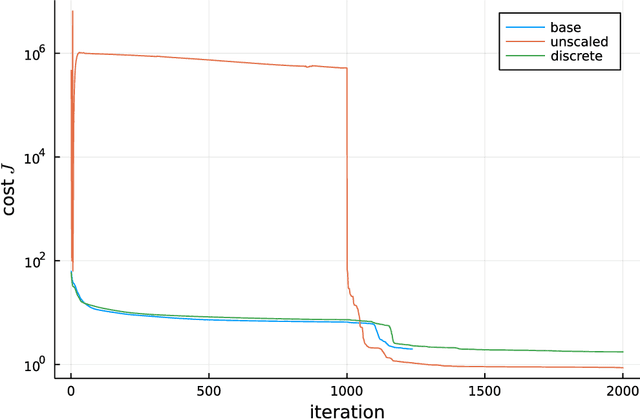
Optimisation of Structured Neural Controller Based on Continuous-Time Policy Gradient

This study presents a policy optimisation framework for structured nonlinear control of continuous-time (deterministic) dynamic systems. The proposed approach prescribes a structure for the controller based on relevant scientific knowledge (such as Lyapunov stability theory or domain experiences) while considering the tunable elements inside the given structure as the point of parametrisation with neural networks. To optimise a cost represented as a function of the neural network weights, the proposed approach utilises the continuous-time policy gradient method based on adjoint sensitivity analysis as a means for correct and performant computation of cost gradient. This enables combining the stability, robustness, and physical interpretability of an analytically-derived structure for the feedback controller with the representational flexibility and optimised resulting performance provided by machine learning techniques. Such a hybrid paradigm for fixed-structure control synthesis is particularly useful for optimising adaptive nonlinear controllers to achieve improved performance in online operation, an area where the existing theory prevails the design of structure while lacking clear analytical understandings about tuning of the gains and the uncertainty model basis functions that govern the performance characteristics. Numerical experiments on aerospace applications illustrate the utility of the structured nonlinear controller optimisation framework.