Debiasing of Two-Line Element Sets for Batch Least Squares Pseudo-Orbit Determination in MEO and GEO

The availability of accurate and timely state predictions for objects in near-Earth orbits is becoming increasingly important due to the growing congestion in key orbital regimes. The Two-line Element Set (TLE) catalogue remains, to this day, one of the few publicly-available, comprehensive sources of near-Earth object ephemerides. At the same time, TLEs are affected by measurement noise and are limited by the low accuracy of the SGP4 theory, introducing significant uncertainty into state predictions. Previous literature has shown that filtering TLEs with batch least squares methods can yield significant improvements in long-term state prediction accuracy. However, this process can be highly sensitive to TLE quality which can vary throughout the year. In this study, it is shown that either extended-duration fit windows of the order of months, or the removal of systematic biases in along-track position prior to state estimation can produce significant reductions in post-fit position errors. Simple models for estimating these systematic biases are shown to be effective without introducing the need for high-complexity Machine Learning (ML) models. Furthermore, by establishing a TLE-based error metric, the need for high accuracy ephemerides is removed when creating these models. For selected satellites in the Medium Earth Orbit (MEO) regime, post-fit position errors are reduced by up to 80 %, from approximately 5 km to 1 km; meanwhile, for selected satellites in the Geostationary Earth Orbit (GEO)/Geosynchronous Earth Orbit (GSO) regime, large oscillations in post-fit position error can be suppressed.

Density Estimation for Entry Guidance Problems using Deep Learning

This work presents a deep-learning approach to estimate atmospheric density profiles for use in planetary entry guidance problems. A long short-term memory (LSTM) neural network is trained to learn the mapping between measurements available onboard an entry vehicle and the density profile through which it is flying. Measurements include the spherical state representation, Cartesian sensed acceleration components, and a surface-pressure measurement. Training data for the network is initially generated by performing a Monte Carlo analysis of an entry mission at Mars using the fully numerical predictor-corrector guidance (FNPEG) algorithm that utilizes an exponential density model, while the truth density profiles are sampled from MarsGRAM. A curriculum learning procedure is developed to refine the LSTM network's predictions for integration within the FNPEG algorithm. The trained LSTM is capable of both predicting the density profile through which the vehicle will fly and reconstructing the density profile through which it has already flown. The performance of the FNPEG algorithm is assessed for three different density estimation techniques: an exponential model, an exponential model augmented with a first-order fading-memory filter, and the LSTM network. Results demonstrate that using the LSTM model results in superior terminal accuracy compared to the other two techniques when considering both noisy and noiseless measurements.

Incremental Correction in Dynamic Systems Modelled with Neural Networks for Constraint Satisfaction

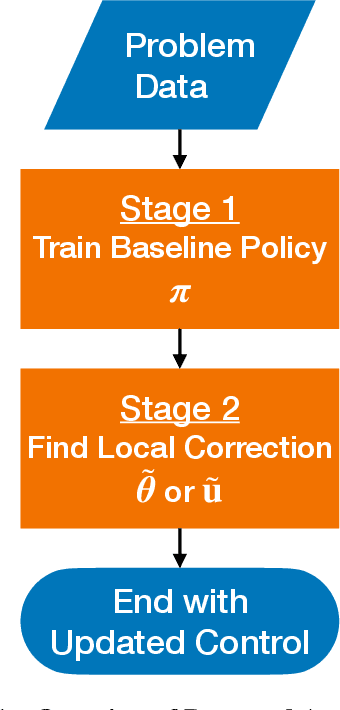
This study presents incremental correction methods for refining neural network parameters or control functions entering into a continuous-time dynamic system to achieve improved solution accuracy in satisfying the interim point constraints placed on the performance output variables. The proposed approach is to linearise the dynamics around the baseline values of its arguments, and then to solve for the corrective input required to transfer the perturbed trajectory to precisely known or desired values at specific time points, i.e., the interim points. Depending on the type of decision variables to adjust, parameter correction and control function correction methods are developed. These incremental correction methods can be utilised as a means to compensate for the prediction errors of pre-trained neural networks in real-time applications where high accuracy of the prediction of dynamical systems at prescribed time points is imperative. In this regard, the online update approach can be useful for enhancing overall targeting accuracy of finite-horizon control subject to point constraints using a neural policy. Numerical example demonstrates the effectiveness of the proposed approach in an application to a powered descent problem at Mars.