MapTrace: Scalable Data Generation for Route Tracing on Maps

While Multimodal Large Language Models have achieved human-like performance on many visual and textual reasoning tasks, their proficiency in fine-grained spatial understanding, such as route tracing on maps remains limited. Unlike humans, who can quickly learn to parse and navigate maps, current models often fail to respect fundamental path constraints, in part due to the prohibitive cost and difficulty of collecting large-scale, pixel-accurate path annotations. To address this, we introduce a scalable synthetic data generation pipeline that leverages synthetic map images and pixel-level parsing to automatically produce precise annotations for this challenging task. Using this pipeline, we construct a fine-tuning dataset of 23k path samples across 4k maps, enabling models to acquire more human-like spatial capabilities. Using this dataset, we fine-tune both open-source and proprietary MLLMs. Results on MapBench show that finetuning substantially improves robustness, raising success rates by up to 6.4 points, while also reducing path-tracing error (NDTW). These gains highlight that fine-grained spatial reasoning, absent in pretrained models, can be explicitly taught with synthetic supervision.

Human Hands as Probes for Interactive Object Understanding

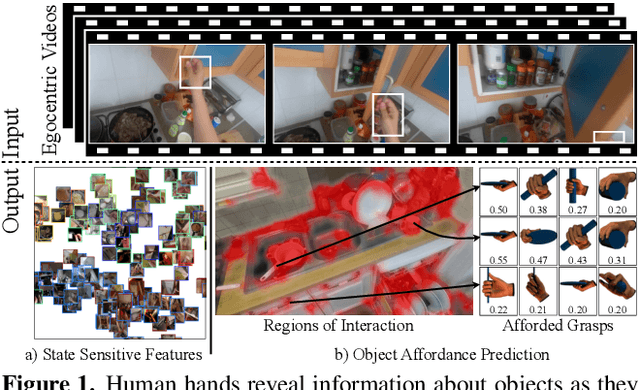
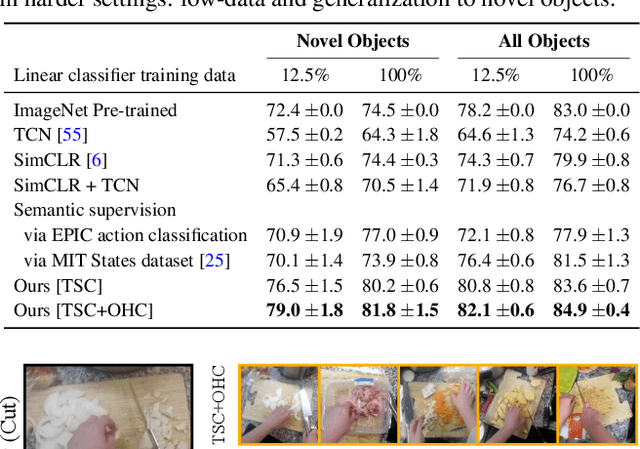
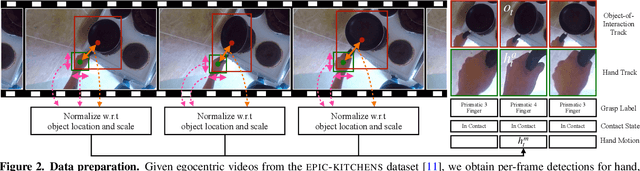
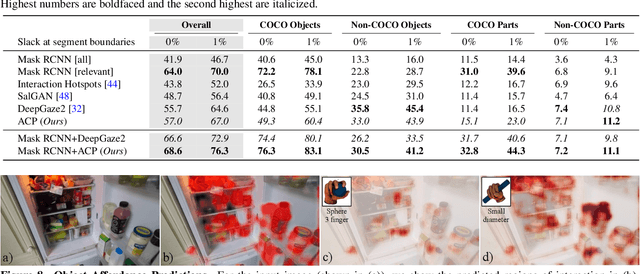
Interactive object understanding, or what we can do to objects and how is a long-standing goal of computer vision. In this paper, we tackle this problem through observation of human hands in in-the-wild egocentric videos. We demonstrate that observation of what human hands interact with and how can provide both the relevant data and the necessary supervision. Attending to hands, readily localizes and stabilizes active objects for learning and reveals places where interactions with objects occur. Analyzing the hands shows what we can do to objects and how. We apply these basic principles on the EPIC-KITCHENS dataset, and successfully learn state-sensitive features, and object affordances (regions of interaction and afforded grasps), purely by observing hands in egocentric videos.

DZip: improved general-purpose lossless compression based on novel neural network modeling

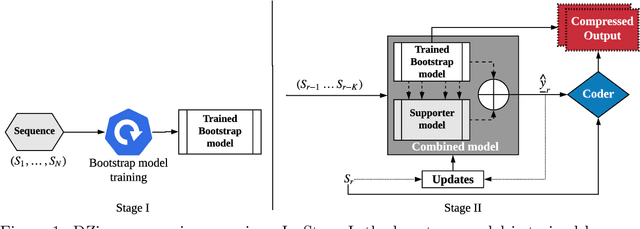
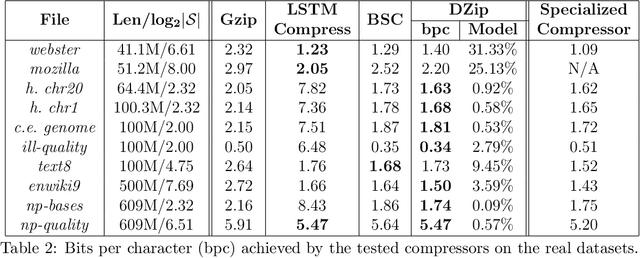
We consider lossless compression based on statistical data modeling followed by prediction-based encoding, where an accurate statistical model for the input data leads to substantial improvements in compression. We propose DZip, a general-purpose compressor for sequential data that exploits the well-known modeling capabilities of neural networks (NNs) for prediction, followed by arithmetic coding. Dzip uses a novel hybrid architecture based on adaptive and semi-adaptive training. Unlike most NN based compressors, DZip does not require additional training data and is not restricted to specific data types, only needing the alphabet size of the input data. The proposed compressor outperforms general-purpose compressors such as Gzip (on average 26% reduction) on a variety of real datasets, achieves near-optimal compression on synthetic datasets, and performs close to specialized compressors for large sequence lengths, without any human input. The main limitation of DZip in its current implementation is the encoding/decoding time, which limits its practicality. Nevertheless, the results showcase the potential of developing improved general-purpose compressors based on neural networks and hybrid modeling.

Learning Activation Functions: A new paradigm for understanding Neural Networks

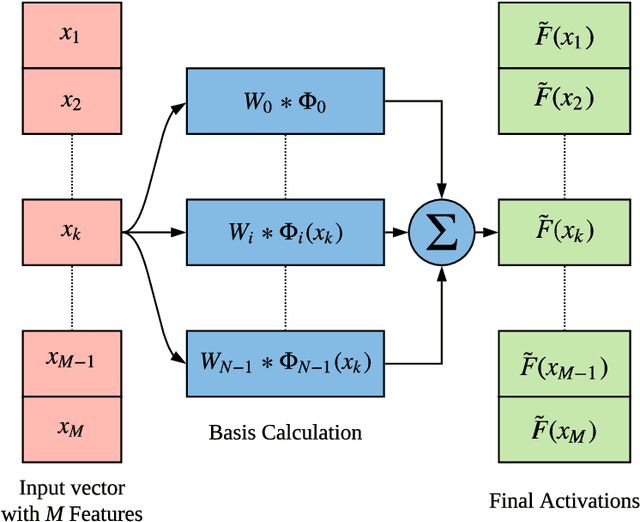
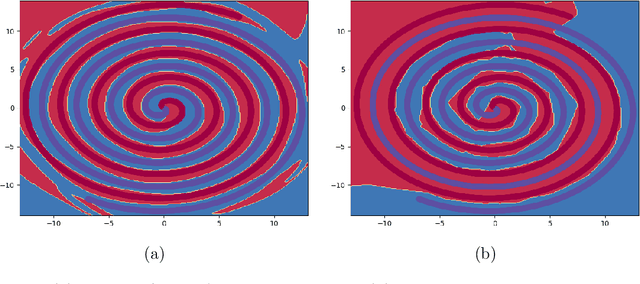
The scope of research in the domain of activation functions remains limited and centered around improving the ease of optimization or generalization quality of neural networks (NNs). However, to develop a deeper understanding of deep learning, it becomes important to look at the non linear component of NNs more carefully. In this paper, we aim to provide a generic form of activation function along with appropriate mathematical grounding so as to allow for insights into the working of NNs in future. We propose ``Self-Learnable Activation Functions'' (SLAF), which are learned during training and are capable of approximating most of the existing activation functions. SLAF is given as a weighted sum of pre-defined basis elements which can serve for a good approximation of the optimal activation function. The coefficients for these basis elements allow a search in the entire space of continuous functions (consisting of all the conventional activations). We propose various training routines which can be used to achieve performance with SLAF equipped neural networks (SLNNs). We prove that SLNNs can approximate any neural network with lipschitz continuous activations, to any arbitrary error highlighting their capacity and possible equivalence with standard NNs. Also, SLNNs can be completely represented as a collections of finite degree polynomial upto the very last layer obviating several hyper parameters like width and depth. Since the optimization of SLNNs is still a challenge, we show that using SLAF along with standard activations (like ReLU) can provide performance improvements with only a small increase in number of parameters.

DeepZip: Lossless Data Compression using Recurrent Neural Networks

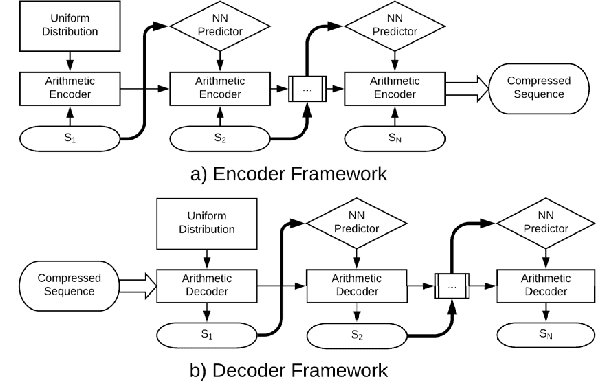
Sequential data is being generated at an unprecedented pace in various forms, including text and genomic data. This creates the need for efficient compression mechanisms to enable better storage, transmission and processing of such data. To solve this problem, many of the existing compressors attempt to learn models for the data and perform prediction-based compression. Since neural networks are known as universal function approximators with the capability to learn arbitrarily complex mappings, and in practice show excellent performance in prediction tasks, we explore and devise methods to compress sequential data using neural network predictors. We combine recurrent neural network predictors with an arithmetic coder and losslessly compress a variety of synthetic, text and genomic datasets. The proposed compressor outperforms Gzip on the real datasets and achieves near-optimal compression for the synthetic datasets. The results also help understand why and where neural networks are good alternatives for traditional finite context models