Unsupervised Motion Representation Learning with Capsule Autoencoders

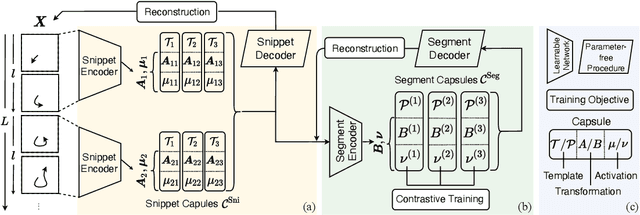
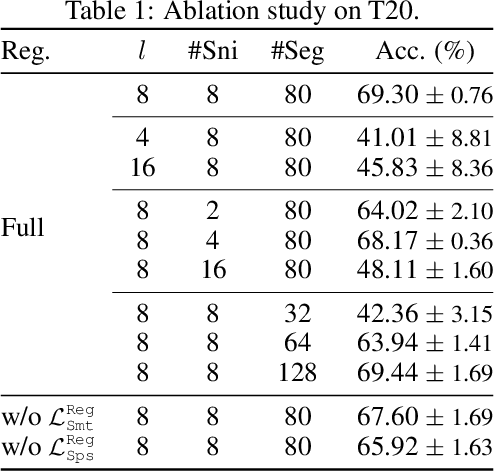
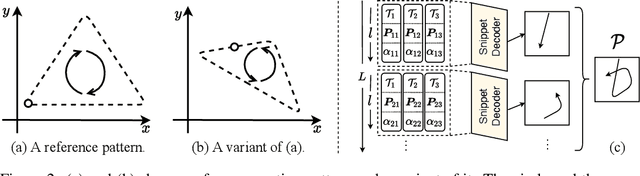
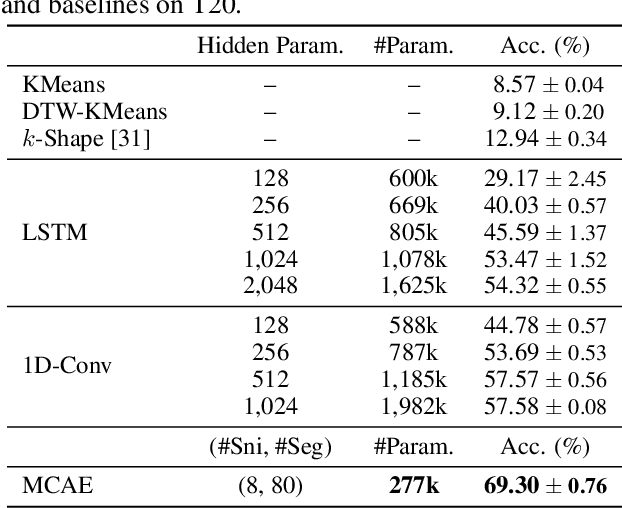
We propose the Motion Capsule Autoencoder (MCAE), which addresses a key challenge in the unsupervised learning of motion representations: transformation invariance. MCAE models motion in a two-level hierarchy. In the lower level, a spatio-temporal motion signal is divided into short, local, and semantic-agnostic snippets. In the higher level, the snippets are aggregated to form full-length semantic-aware segments. For both levels, we represent motion with a set of learned transformation invariant templates and the corresponding geometric transformations by using capsule autoencoders of a novel design. This leads to a robust and efficient encoding of viewpoint changes. MCAE is evaluated on a novel Trajectory20 motion dataset and various real-world skeleton-based human action datasets. Notably, it achieves better results than baselines on Trajectory20 with considerably fewer parameters and state-of-the-art performance on the unsupervised skeleton-based action recognition task.

Semantically-Regularized Logic Graph Embeddings

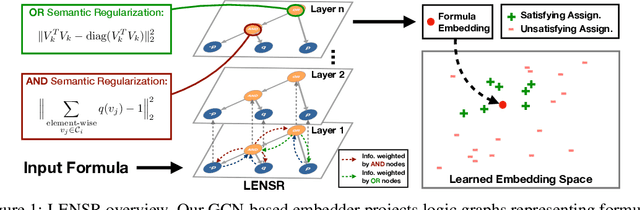
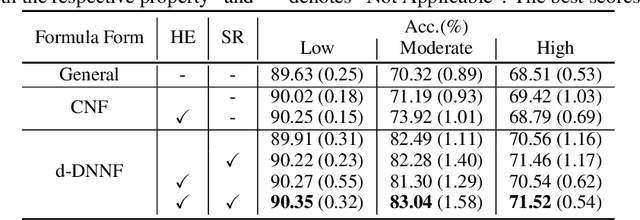
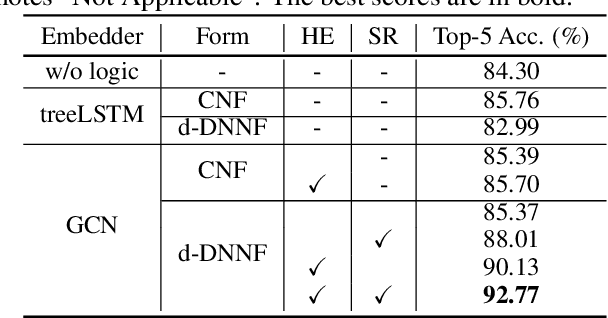
In this work, we aim to utilize prior knowledge encoded as logical rules to improve the performance of deep models. We propose a logic graph embedding network that projects d-DNNF formulae (and assignments) onto a manifold via an augmented Graph Convolutional Network (GCN). To generate semantically-faithful embeddings, we propose techniques to recognize node heterogeneity, and semantic regularization that incorporate structural constraints into the embedding. Experiments show that our approach improves the performance of models trained to perform model-checking and visual relation prediction.

Group $K$-Means

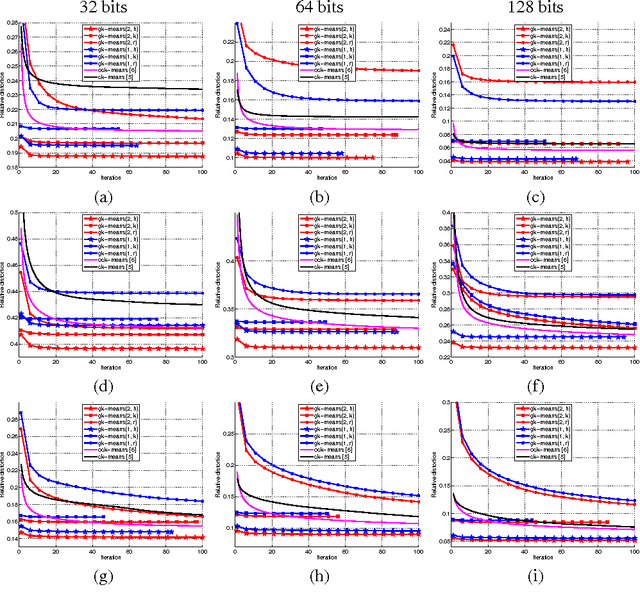
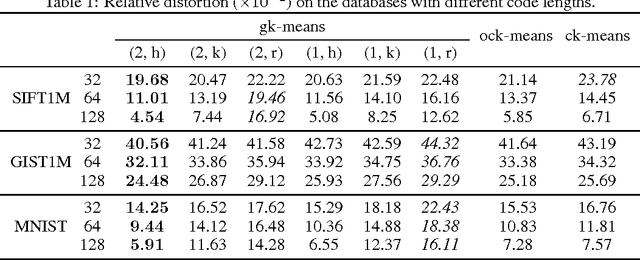
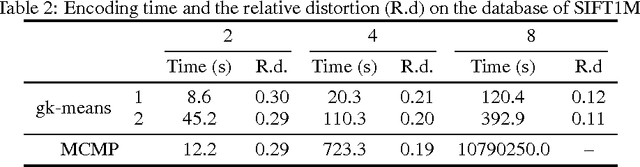
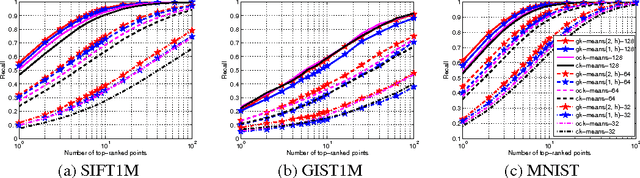
We study how to learn multiple dictionaries from a dataset, and approximate any data point by the sum of the codewords each chosen from the corresponding dictionary. Although theoretically low approximation errors can be achieved by the global solution, an effective solution has not been well studied in practice. To solve the problem, we propose a simple yet effective algorithm \textit{Group $K$-Means}. Specifically, we take each dictionary, or any two selected dictionaries, as a group of $K$-means cluster centers, and then deal with the approximation issue by minimizing the approximation errors. Besides, we propose a hierarchical initialization for such a non-convex problem. Experimental results well validate the effectiveness of the approach.