Minhua Chen
Duke University
Deep Clustering with Measure Propagation
Apr 26, 2021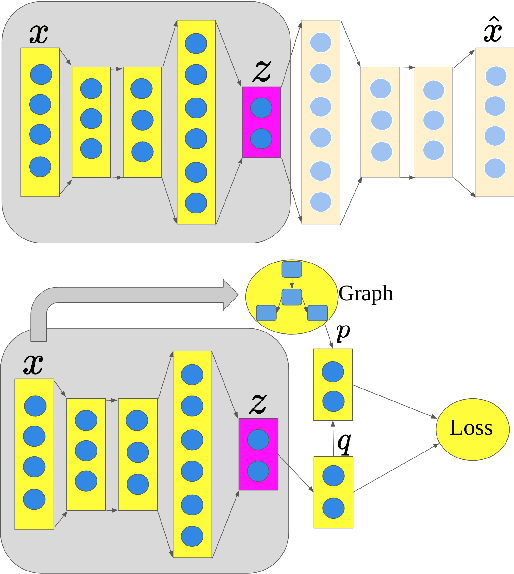

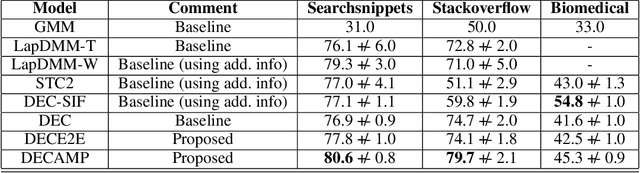
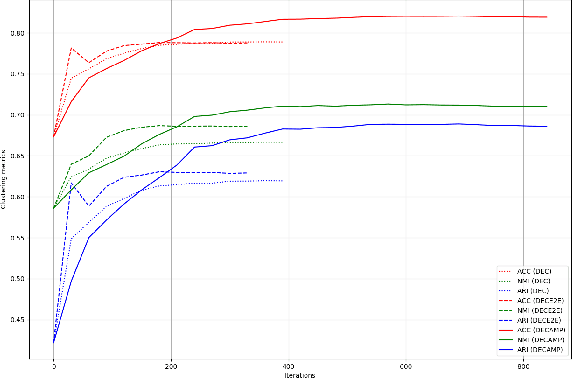
Abstract:Deep models have improved state-of-the-art for both supervised and unsupervised learning. For example, deep embedded clustering (DEC) has greatly improved the unsupervised clustering performance, by using stacked autoencoders for representation learning. However, one weakness of deep modeling is that the local neighborhood structure in the original space is not necessarily preserved in the latent space. To preserve local geometry, various methods have been proposed in the supervised and semi-supervised learning literature (e.g., spectral clustering and label propagation) using graph Laplacian regularization. In this paper, we combine the strength of deep representation learning with measure propagation (MP), a KL-divergence based graph regularization method originally used in the semi-supervised scenario. The main assumption of MP is that if two data points are close in the original space, they are likely to belong to the same class, measured by KL-divergence of class membership distribution. By taking the same assumption in the unsupervised learning scenario, we propose our Deep Embedded Clustering Aided by Measure Propagation (DECAMP) model. We evaluate DECAMP on short text clustering tasks. On three public datasets, DECAMP performs competitively with other state-of-the-art baselines, including baselines using additional data to generate word embeddings used in the clustering process. As an example, on the Stackoverflow dataset, DECAMP achieved a clustering accuracy of 79%, which is about 5% higher than all existing baselines. These empirical results suggest that DECAMP is a very effective method for unsupervised learning.
Faithful Variable Screening for High-Dimensional Convex Regression
Nov 18, 2014



Abstract:We study the problem of variable selection in convex nonparametric regression. Under the assumption that the true regression function is convex and sparse, we develop a screening procedure to select a subset of variables that contains the relevant variables. Our approach is a two-stage quadratic programming method that estimates a sum of one-dimensional convex functions, followed by one-dimensional concave regression fits on the residuals. In contrast to previous methods for sparse additive models, the optimization is finite dimensional and requires no tuning parameters for smoothness. Under appropriate assumptions, we prove that the procedure is faithful in the population setting, yielding no false negatives. We give a finite sample statistical analysis, and introduce algorithms for efficiently carrying out the required quadratic programs. The approach leads to computational and statistical advantages over fitting a full model, and provides an effective, practical approach to variable screening in convex regression.
Communications Inspired Linear Discriminant Analysis
Jun 27, 2012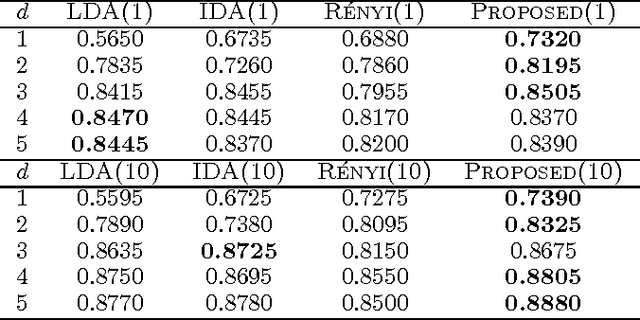

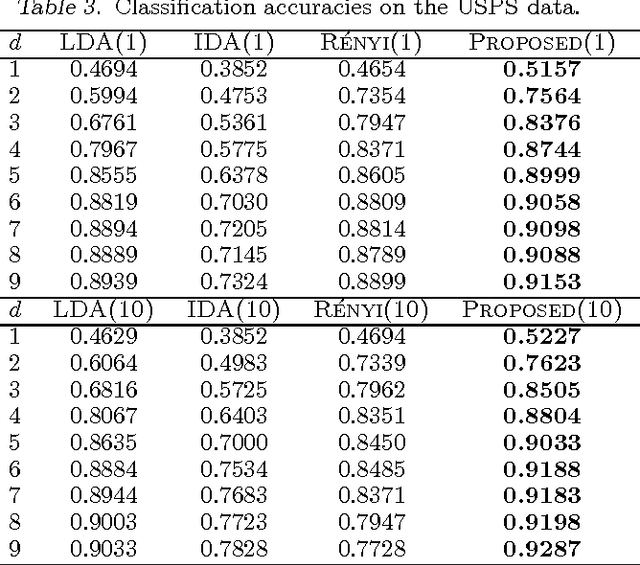
Abstract:We study the problem of supervised linear dimensionality reduction, taking an information-theoretic viewpoint. The linear projection matrix is designed by maximizing the mutual information between the projected signal and the class label (based on a Shannon entropy measure). By harnessing a recent theoretical result on the gradient of mutual information, the above optimization problem can be solved directly using gradient descent, without requiring simplification of the objective function. Theoretical analysis and empirical comparison are made between the proposed method and two closely related methods (Linear Discriminant Analysis and Information Discriminant Analysis), and comparisons are also made with a method in which Renyi entropy is used to define the mutual information (in this case the gradient may be computed simply, under a special parameter setting). Relative to these alternative approaches, the proposed method achieves promising results on real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge