Deep Clustering with Measure Propagation
Paper and Code
Apr 26, 2021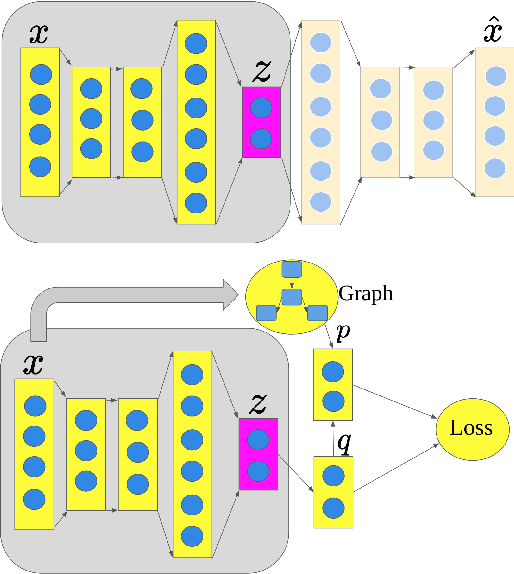

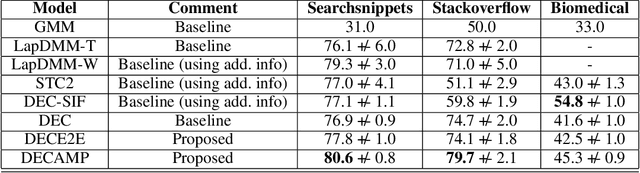
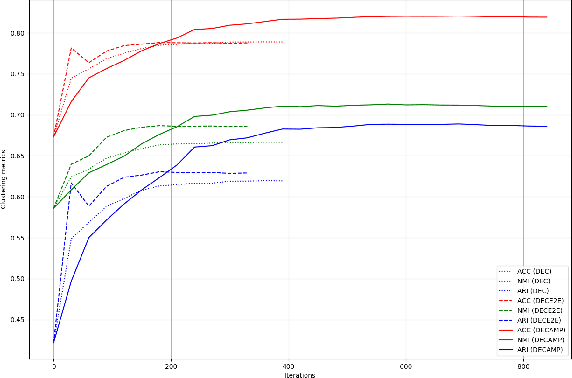
Deep models have improved state-of-the-art for both supervised and unsupervised learning. For example, deep embedded clustering (DEC) has greatly improved the unsupervised clustering performance, by using stacked autoencoders for representation learning. However, one weakness of deep modeling is that the local neighborhood structure in the original space is not necessarily preserved in the latent space. To preserve local geometry, various methods have been proposed in the supervised and semi-supervised learning literature (e.g., spectral clustering and label propagation) using graph Laplacian regularization. In this paper, we combine the strength of deep representation learning with measure propagation (MP), a KL-divergence based graph regularization method originally used in the semi-supervised scenario. The main assumption of MP is that if two data points are close in the original space, they are likely to belong to the same class, measured by KL-divergence of class membership distribution. By taking the same assumption in the unsupervised learning scenario, we propose our Deep Embedded Clustering Aided by Measure Propagation (DECAMP) model. We evaluate DECAMP on short text clustering tasks. On three public datasets, DECAMP performs competitively with other state-of-the-art baselines, including baselines using additional data to generate word embeddings used in the clustering process. As an example, on the Stackoverflow dataset, DECAMP achieved a clustering accuracy of 79%, which is about 5% higher than all existing baselines. These empirical results suggest that DECAMP is a very effective method for unsupervised learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge