Deep Learning in Target Space

Deep learning uses neural networks which are parameterised by their weights. The neural networks are usually trained by tuning the weights to directly minimise a given loss function. In this paper we propose to reparameterise the weights into targets for the firing strengths of the individual nodes in the network. Given a set of targets, it is possible to calculate the weights which make the firing strengths best meet those targets. It is argued that using targets for training addresses the problem of exploding gradients, by a process which we call cascade untangling, and makes the loss-function surface smoother to traverse, and so leads to easier, faster training, and also potentially better generalisation, of the neural network. It also allows for easier learning of deeper and recurrent network structures. The necessary conversion of targets to weights comes at an extra computational expense, which is in many cases manageable. Learning in target space can be combined with existing neural-network optimisers, for extra gain. Experimental results show the speed of using target space, and examples of improved generalisation, for fully-connected networks and convolutional networks, and the ability to recall and process long time sequences and perform natural-language processing with recurrent networks.

Optimal resampling for the noisy OneMax problem

The OneMax problem is a standard benchmark optimisation problem for a binary search space. Recent work on applying a Bandit-Based Random Mutation Hill-Climbing algorithm to the noisy OneMax Problem showed that it is important to choose a good value for the resampling number to make a careful trade off between taking more samples in order to reduce noise, and taking fewer samples to reduce the total computational cost. This paper extends that observation, by deriving an analytical expression for the running time of the RMHC algorithm with resampling applied to the noisy OneMax problem, and showing both theoretically and empirically that the optimal resampling number increases with the number of dimensions in the search space.

The Importance of Clipping in Neurocontrol by Direct Gradient Descent on the Cost-to-Go Function and in Adaptive Dynamic Programming

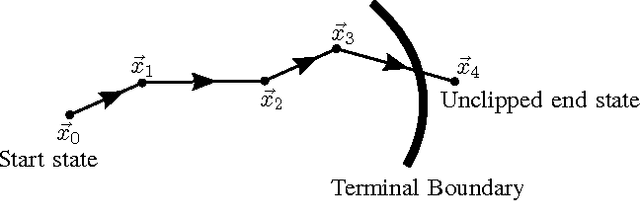
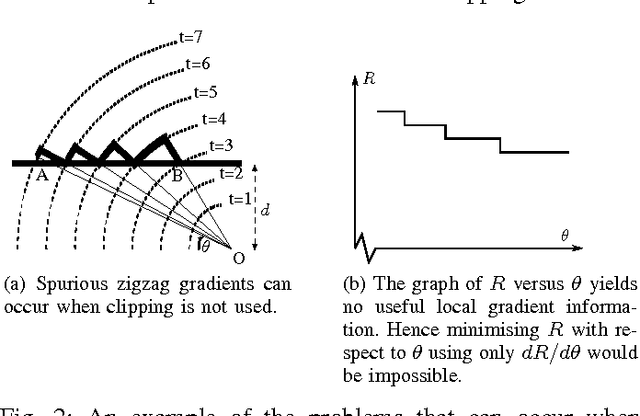
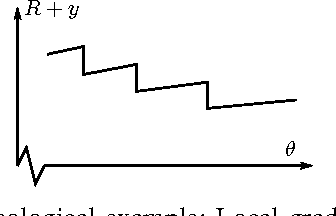
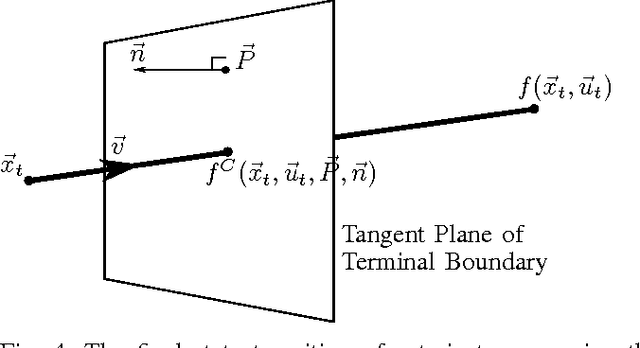
In adaptive dynamic programming, neurocontrol and reinforcement learning, the objective is for an agent to learn to choose actions so as to minimise a total cost function. In this paper we show that when discretized time is used to model the motion of the agent, it can be very important to do "clipping" on the motion of the agent in the final time step of the trajectory. By clipping we mean that the final time step of the trajectory is to be truncated such that the agent stops exactly at the first terminal state reached, and no distance further. We demonstrate that when clipping is omitted, learning performance can fail to reach the optimum; and when clipping is done properly, learning performance can improve significantly. The clipping problem we describe affects algorithms which use explicit derivatives of the model functions of the environment to calculate a learning gradient. These include Backpropagation Through Time for Control, and methods based on Dual Heuristic Dynamic Programming. However the clipping problem does not significantly affect methods based on Heuristic Dynamic Programming, Temporal Differences or Policy Gradient Learning algorithms. Similarly, the clipping problem does not affect fixed-length finite-horizon problems.

The Divergence of Reinforcement Learning Algorithms with Value-Iteration and Function Approximation

This paper gives specific divergence examples of value-iteration for several major Reinforcement Learning and Adaptive Dynamic Programming algorithms, when using a function approximator for the value function. These divergence examples differ from previous divergence examples in the literature, in that they are applicable for a greedy policy, i.e. in a "value iteration" scenario. Perhaps surprisingly, with a greedy policy, it is also possible to get divergence for the algorithms TD(1) and Sarsa(1). In addition to these divergences, we also achieve divergence for the Adaptive Dynamic Programming algorithms HDP, DHP and GDHP.

The Local Optimality of Reinforcement Learning by Value Gradients, and its Relationship to Policy Gradient Learning

In this theoretical paper we are concerned with the problem of learning a value function by a smooth general function approximator, to solve a deterministic episodic control problem in a large continuous state space. It is shown that learning the gradient of the value-function at every point along a trajectory generated by a greedy policy is a sufficient condition for the trajectory to be locally extremal, and often locally optimal, and we argue that this brings greater efficiency to value-function learning. This contrasts to traditional value-function learning in which the value-function must be learnt over the whole of state space. It is also proven that policy-gradient learning applied to a greedy policy on a value-function produces a weight update equivalent to a value-gradient weight update, which provides a surprising connection between these two alternative paradigms of reinforcement learning, and a convergence proof for control problems with a value function represented by a general smooth function approximator.

Reinforcement Learning by Value Gradients

The concept of the value-gradient is introduced and developed in the context of reinforcement learning. It is shown that by learning the value-gradients exploration or stochastic behaviour is no longer needed to find locally optimal trajectories. This is the main motivation for using value-gradients, and it is argued that learning value-gradients is the actual objective of any value-function learning algorithm for control problems. It is also argued that learning value-gradients is significantly more efficient than learning just the values, and this argument is supported in experiments by efficiency gains of several orders of magnitude, in several problem domains. Once value-gradients are introduced into learning, several analyses become possible. For example, a surprising equivalence between a value-gradient learning algorithm and a policy-gradient learning algorithm is proven, and this provides a robust convergence proof for control problems using a value function with a general function approximator.