The Importance of Clipping in Neurocontrol by Direct Gradient Descent on the Cost-to-Go Function and in Adaptive Dynamic Programming

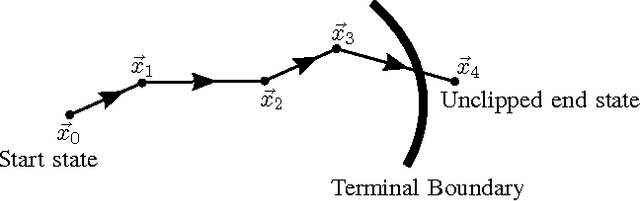
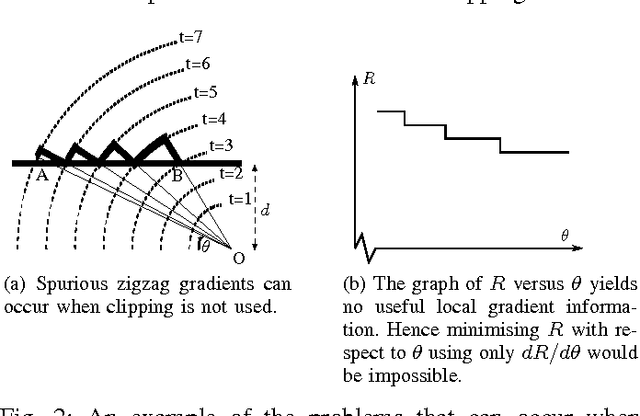
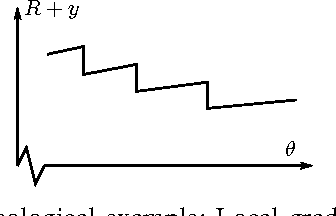
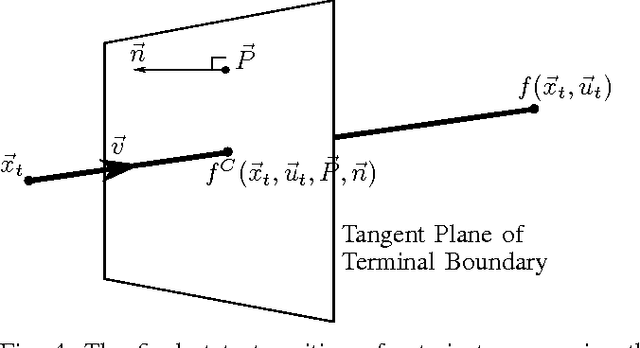
In adaptive dynamic programming, neurocontrol and reinforcement learning, the objective is for an agent to learn to choose actions so as to minimise a total cost function. In this paper we show that when discretized time is used to model the motion of the agent, it can be very important to do "clipping" on the motion of the agent in the final time step of the trajectory. By clipping we mean that the final time step of the trajectory is to be truncated such that the agent stops exactly at the first terminal state reached, and no distance further. We demonstrate that when clipping is omitted, learning performance can fail to reach the optimum; and when clipping is done properly, learning performance can improve significantly. The clipping problem we describe affects algorithms which use explicit derivatives of the model functions of the environment to calculate a learning gradient. These include Backpropagation Through Time for Control, and methods based on Dual Heuristic Dynamic Programming. However the clipping problem does not significantly affect methods based on Heuristic Dynamic Programming, Temporal Differences or Policy Gradient Learning algorithms. Similarly, the clipping problem does not affect fixed-length finite-horizon problems.