Stability and Generalization for Distributed SGDA

Minimax optimization is gaining increasing attention in modern machine learning applications. Driven by large-scale models and massive volumes of data collected from edge devices, as well as the concern to preserve client privacy, communication-efficient distributed minimax optimization algorithms become popular, such as Local Stochastic Gradient Descent Ascent (Local-SGDA), and Local Decentralized SGDA (Local-DSGDA). While most existing research on distributed minimax algorithms focuses on convergence rates, computation complexity, and communication efficiency, the generalization performance remains underdeveloped, whereas generalization ability is a pivotal indicator for evaluating the holistic performance of a model when fed with unknown data. In this paper, we propose the stability-based generalization analytical framework for Distributed-SGDA, which unifies two popular distributed minimax algorithms including Local-SGDA and Local-DSGDA, and conduct a comprehensive analysis of stability error, generalization gap, and population risk across different metrics under various settings, e.g., (S)C-(S)C, PL-SC, and NC-NC cases. Our theoretical results reveal the trade-off between the generalization gap and optimization error and suggest hyperparameters choice to obtain the optimal population risk. Numerical experiments for Local-SGDA and Local-DSGDA validate the theoretical results.

Stability and Generalization of the Decentralized Stochastic Gradient Descent Ascent Algorithm

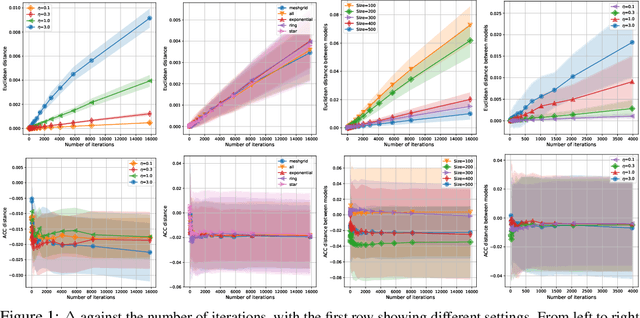
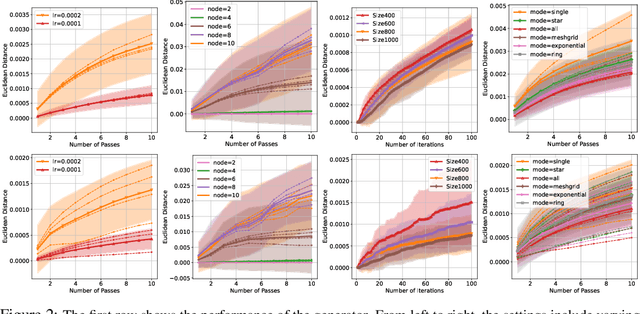
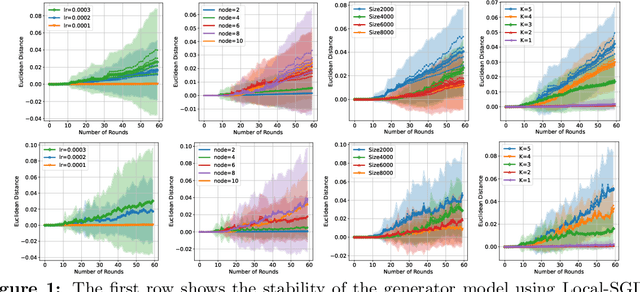
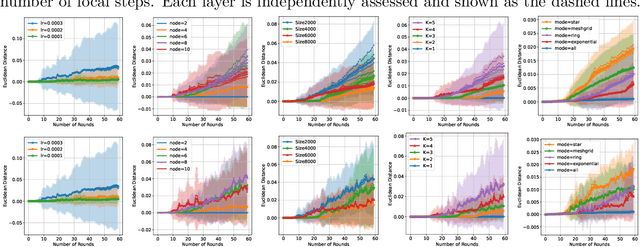
The growing size of available data has attracted increasing interest in solving minimax problems in a decentralized manner for various machine learning tasks. Previous theoretical research has primarily focused on the convergence rate and communication complexity of decentralized minimax algorithms, with little attention given to their generalization. In this paper, we investigate the primal-dual generalization bound of the decentralized stochastic gradient descent ascent (D-SGDA) algorithm using the approach of algorithmic stability under both convex-concave and nonconvex-nonconcave settings. Our theory refines the algorithmic stability in a decentralized manner and demonstrates that the decentralized structure does not destroy the stability and generalization of D-SGDA, implying that it can generalize as well as the vanilla SGDA in certain situations. Our results analyze the impact of different topologies on the generalization bound of the D-SGDA algorithm beyond trivial factors such as sample sizes, learning rates, and iterations. We also evaluate the optimization error and balance it with the generalization gap to obtain the optimal population risk of D-SGDA in the convex-concave setting. Additionally, we perform several numerical experiments which validate our theoretical findings.

Zero-Shot Sharpness-Aware Quantization for Pre-trained Language Models

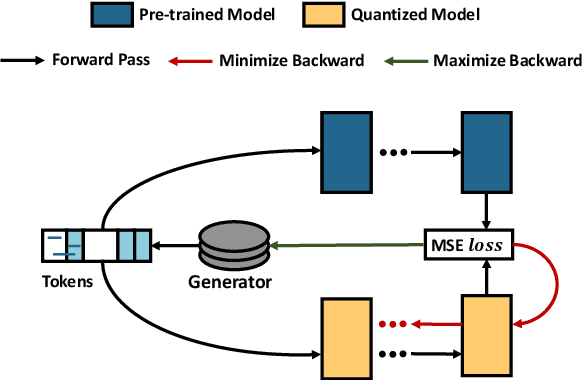
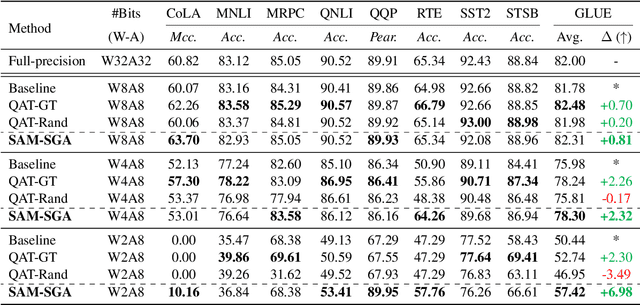
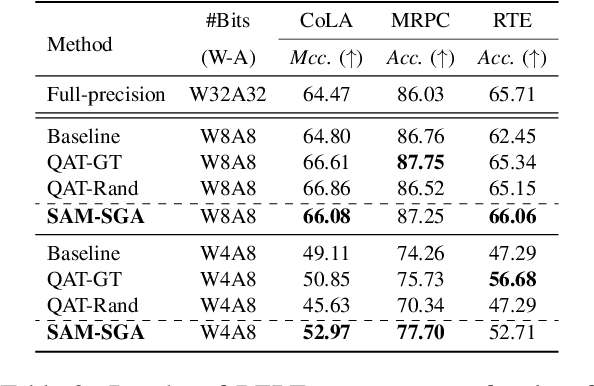
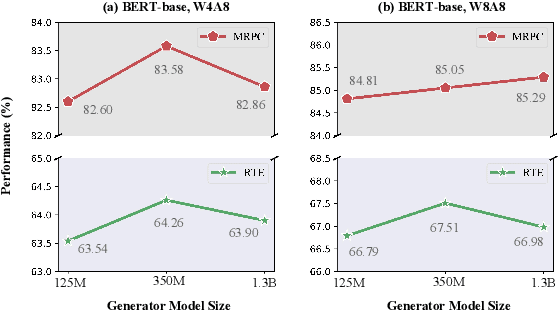
Quantization is a promising approach for reducing memory overhead and accelerating inference, especially in large pre-trained language model (PLM) scenarios. While having no access to original training data due to security and privacy concerns has emerged the demand for zero-shot quantization. Most of the cutting-edge zero-shot quantization methods primarily 1) apply to computer vision tasks, and 2) neglect of overfitting problem in the generative adversarial learning process, leading to sub-optimal performance. Motivated by this, we propose a novel zero-shot sharpness-aware quantization (ZSAQ) framework for the zero-shot quantization of various PLMs. The key algorithm in solving ZSAQ is the SAM-SGA optimization, which aims to improve the quantization accuracy and model generalization via optimizing a minimax problem. We theoretically prove the convergence rate for the minimax optimization problem and this result can be applied to other nonconvex-PL minimax optimization frameworks. Extensive experiments on 11 tasks demonstrate that our method brings consistent and significant performance gains on both discriminative and generative PLMs, i.e., up to +6.98 average score. Furthermore, we empirically validate that our method can effectively improve the model generalization.

Robust Generalization against Photon-Limited Corruptions via Worst-Case Sharpness Minimization

Robust generalization aims to tackle the most challenging data distributions which are rare in the training set and contain severe noises, i.e., photon-limited corruptions. Common solutions such as distributionally robust optimization (DRO) focus on the worst-case empirical risk to ensure low training error on the uncommon noisy distributions. However, due to the over-parameterized model being optimized on scarce worst-case data, DRO fails to produce a smooth loss landscape, thus struggling on generalizing well to the test set. Therefore, instead of focusing on the worst-case risk minimization, we propose SharpDRO by penalizing the sharpness of the worst-case distribution, which measures the loss changes around the neighbor of learning parameters. Through worst-case sharpness minimization, the proposed method successfully produces a flat loss curve on the corrupted distributions, thus achieving robust generalization. Moreover, by considering whether the distribution annotation is available, we apply SharpDRO to two problem settings and design a worst-case selection process for robust generalization. Theoretically, we show that SharpDRO has a great convergence guarantee. Experimentally, we simulate photon-limited corruptions using CIFAR10/100 and ImageNet30 datasets and show that SharpDRO exhibits a strong generalization ability against severe corruptions and exceeds well-known baseline methods with large performance gains.