Denoising and Reconstruction of Nonlinear Dynamics using Truncated Reservoir Computing

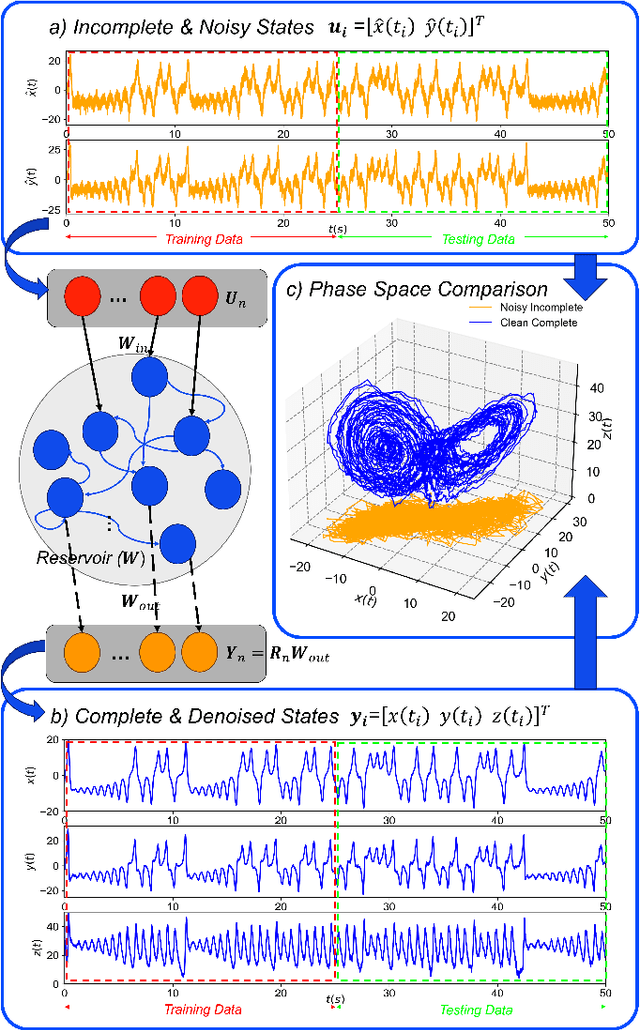
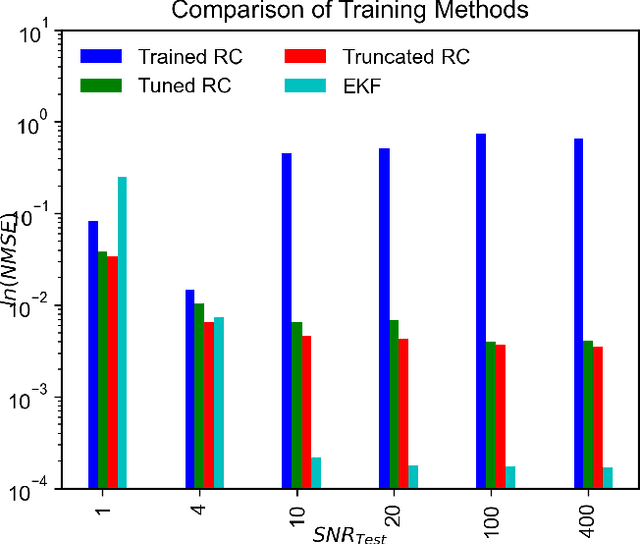
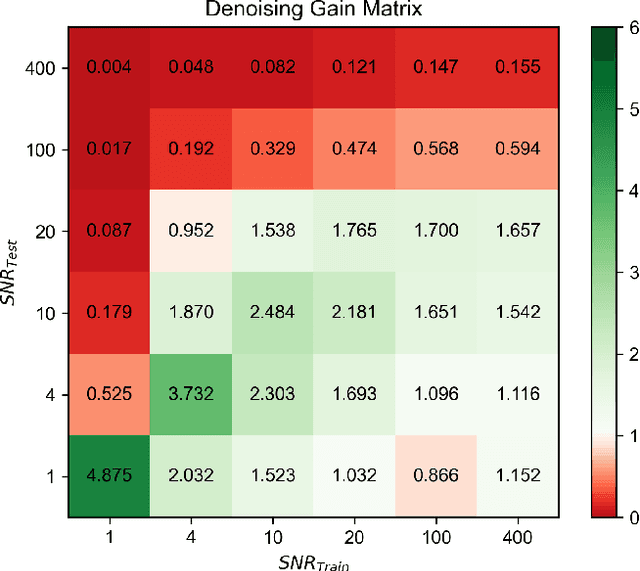
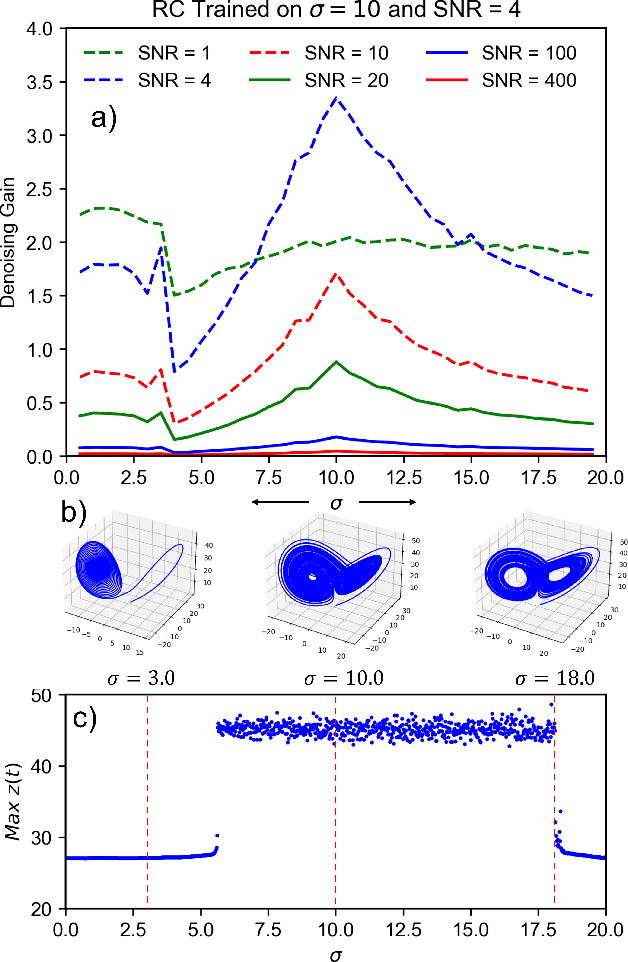
Measurements acquired from distributed physical systems are often sparse and noisy. Therefore, signal processing and system identification tools are required to mitigate noise effects and reconstruct unobserved dynamics from limited sensor data. However, this process is particularly challenging because the fundamental equations governing the dynamics are largely unavailable in practice. Reservoir Computing (RC) techniques have shown promise in efficiently simulating dynamical systems through an unstructured and efficient computation graph comprising a set of neurons with random connectivity. However, the potential of RC to operate in noisy regimes and distinguish noise from the primary dynamics of the system has not been fully explored. This paper presents a novel RC method for noise filtering and reconstructing nonlinear dynamics, offering a novel learning protocol associated with hyperparameter optimization. The performance of the RC in terms of noise intensity, noise frequency content, and drastic shifts in dynamical parameters are studied in two illustrative examples involving the nonlinear dynamics of the Lorenz attractor and adaptive exponential integrate-and-fire system (AdEx). It is shown that the denoising performance improves via truncating redundant nodes and edges of the computing reservoir, as well as properly optimizing the hyperparameters, e.g., the leakage rate, the spectral radius, the input connectivity, and the ridge regression parameter. Furthermore, the presented framework shows good generalization behavior when tested for reconstructing unseen attractors from the bifurcation diagram. Compared to the Extended Kalman Filter (EKF), the presented RC framework yields competitive accuracy at low signal-to-noise ratios (SNRs) and high-frequency ranges.

The impact of AI on engineering design procedures for dynamical systems

Artificial intelligence (AI) is driving transformative changes across numerous fields, revolutionizing conventional processes and creating new opportunities for innovation. The development of mechatronic systems is undergoing a similar transformation. Over the past decade, modeling, simulation, and optimization techniques have become integral to the design process, paving the way for the adoption of AI-based methods. In this paper, we examine the potential for integrating AI into the engineering design process, using the V-model from the VDI guideline 2206, considered the state-of-the-art in product design, as a foundation. We identify and classify AI methods based on their suitability for specific stages within the engineering product design workflow. Furthermore, we present a series of application examples where AI-assisted design has been successfully implemented by the authors. These examples, drawn from research projects within the DFG Priority Program \emph{SPP~2353: Daring More Intelligence - Design Assistants in Mechanics and Dynamics}, showcase a diverse range of applications across mechanics and mechatronics, including areas such as acoustics and robotics.

Data assimilation and parameter identification for water waves using the nonlinear Schrödinger equation and physics-informed neural networks

The measurement of deep water gravity wave elevations using in-situ devices, such as wave gauges, typically yields spatially sparse data. This sparsity arises from the deployment of a limited number of gauges due to their installation effort and high operational costs. The reconstruction of the spatio-temporal extent of surface elevation poses an ill-posed data assimilation problem, challenging to solve with conventional numerical techniques. To address this issue, we propose the application of a physics-informed neural network (PINN), aiming to reconstruct physically consistent wave fields between two designated measurement locations several meters apart. Our method ensures this physical consistency by integrating residuals of the hydrodynamic nonlinear Schr\"{o}dinger equation (NLSE) into the PINN's loss function. Using synthetic wave elevation time series from distinct locations within a wave tank, we initially achieve successful reconstruction quality by employing constant, predetermined NLSE coefficients. However, the reconstruction quality is further improved by introducing NLSE coefficients as additional identifiable variables during PINN training. The results not only showcase a technically relevant application of the PINN method but also represent a pioneering step towards improving the initialization of deterministic wave prediction methods.

Machine learning for phase-resolved reconstruction of nonlinear ocean wave surface elevations from sparse remote sensing data

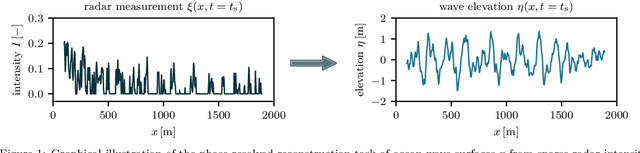
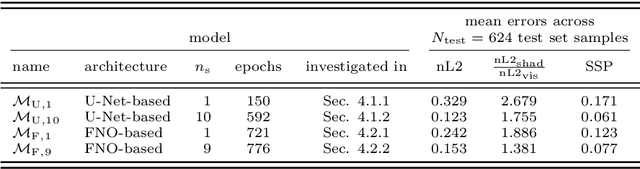
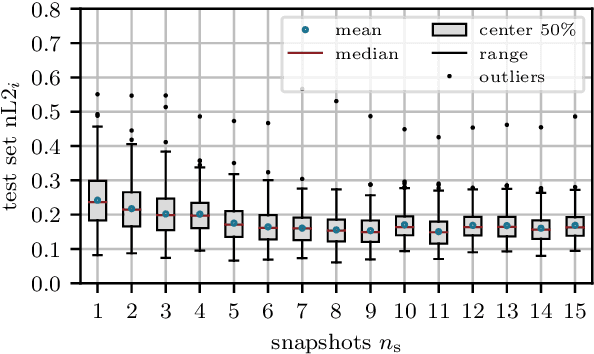
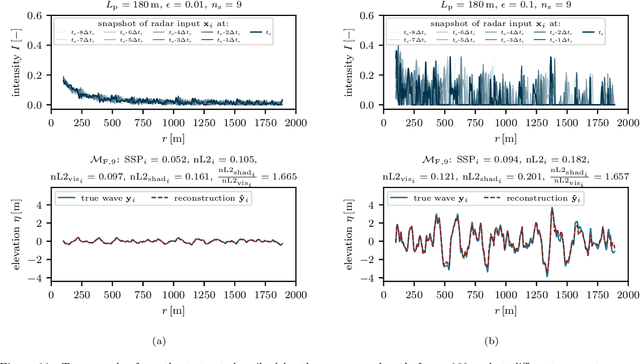
Accurate short-term prediction of phase-resolved water wave conditions is crucial for decision-making in ocean engineering. However, the initialization of remote-sensing-based wave prediction models first requires a reconstruction of wave surfaces from sparse measurements like radar. Existing reconstruction methods either rely on computationally intensive optimization procedures or simplistic modeling assumptions that compromise real-time capability or accuracy of the entire prediction process. We therefore address these issues by proposing a novel approach for phase-resolved wave surface reconstruction using neural networks based on the U-Net and Fourier neural operator (FNO) architectures. Our approach utilizes synthetic yet highly realistic training data on uniform one-dimensional grids, that is generated by the high-order spectral method for wave simulation and a geometric radar modeling approach. The investigation reveals that both models deliver accurate wave reconstruction results and show good generalization for different sea states when trained with spatio-temporal radar data containing multiple historic radar snapshots in each input. Notably, the FNO-based network performs better in handling the data structure imposed by wave physics due to its global approach to learn the mapping between input and desired output in Fourier space.

Surface Similarity Parameter: A New Machine Learning Loss Metric for Oscillatory Spatio-Temporal Data

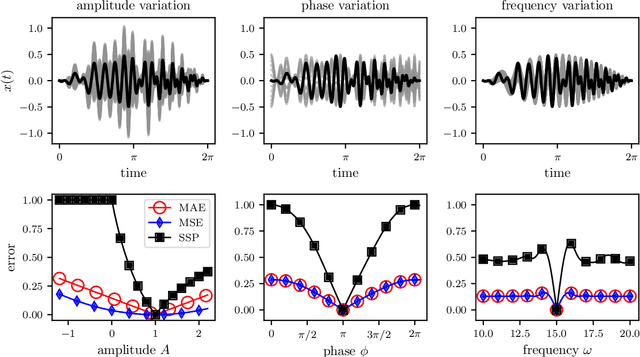
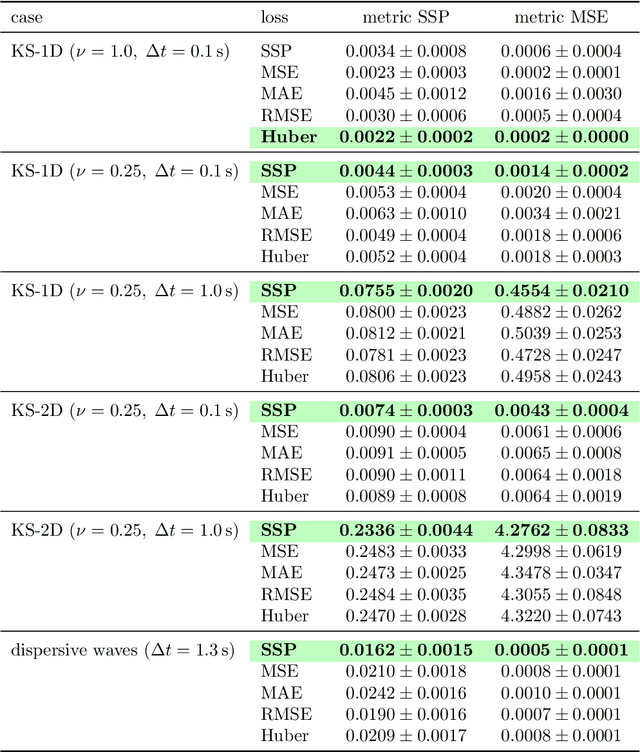
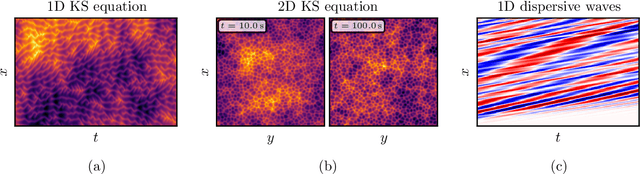
Supervised machine learning approaches require the formulation of a loss functional to be minimized in the training phase. Sequential data are ubiquitous across many fields of research, and are often treated with Euclidean distance-based loss functions that were designed for tabular data. For smooth oscillatory data, those conventional approaches lack the ability to penalize amplitude, frequency and phase prediction errors at the same time, and tend to be biased towards amplitude errors. We introduce the surface similarity parameter (SSP) as a novel loss function that is especially useful for training machine learning models on smooth oscillatory sequences. Our extensive experiments on chaotic spatio-temporal dynamical systems indicate that the SSP is beneficial for shaping gradients, thereby accelerating the training process, reducing the final prediction error, and implementing a stronger regularization effect compared to using classical loss functions. The results indicate the potential of the novel loss metric particularly for highly complex and chaotic data, such as data stemming from the nonlinear two-dimensional Kuramoto-Sivashinsky equation and the linear propagation of dispersive surface gravity waves in fluids.

Deep learning for brake squeal: vibration detection, characterization and prediction

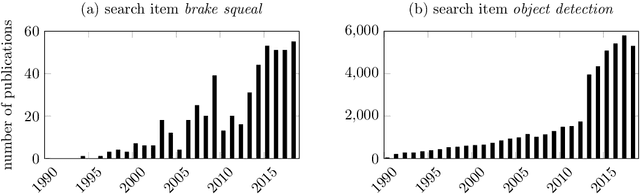
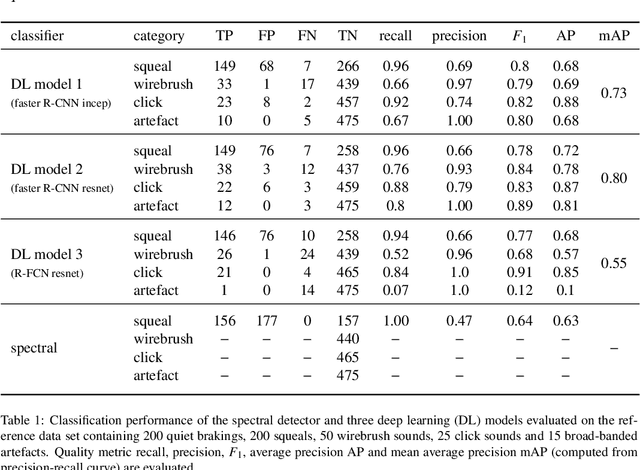
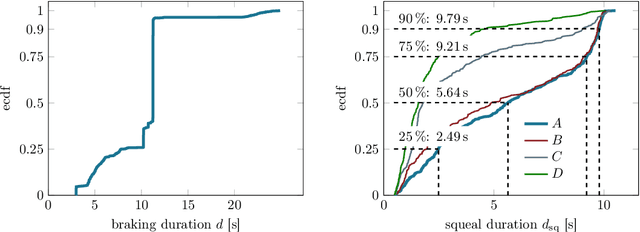
Despite significant advances in numerical modeling of brake squeal, the majority of industrial research and design is still conducted experimentally. In this work we report on novel strategies for handling data-intensive vibration testings and gaining better insights into brake system vibrations. To this end, we propose machine learning-based methods to detect and characterize vibrations, understand sensitivities and predict brake squeal. Our aim is to illustrate how interdisciplinary approaches can leverage the potential of data science techniques for classical mechanical engineering challenges. In the first part, a deep learning brake squeal detector is developed to identify several classes of typical sounds in vibration recordings. The detection method is rooted in recent computer vision techniques for object detection. It allows to overcome limitations of classical approaches that rely on spectral properties of the recorded vibrations. Results indicate superior detection and characterization quality when compared to state-of-the-art brake squeal detectors. In the second part, deep recurrent neural networks are employed to learn the parametric patterns that determine the dynamic stability of the brake system during operation. Given a set of multivariate loading conditions, the models learn to predict the vibrational behavior of the structure. The validated models represent virtual twins for the squeal behavior of a specific brake system. It is found that those models can predict the occurrence and onset of brake squeal with high accuracy. Hence, the deep learning models can identify the complicated patterns and temporal dependencies in the loading conditions that drive the dynamical structure into regimes of instability. Large data sets from commercial brake system testing are used to train and validate the deep learning models.