Machine learning for phase-resolved reconstruction of nonlinear ocean wave surface elevations from sparse remote sensing data

Accurate short-term prediction of phase-resolved water wave conditions is crucial for decision-making in ocean engineering. However, the initialization of remote-sensing-based wave prediction models first requires a reconstruction of wave surfaces from sparse measurements like radar. Existing reconstruction methods either rely on computationally intensive optimization procedures or simplistic modeling assumptions that compromise real-time capability or accuracy of the entire prediction process. We therefore address these issues by proposing a novel approach for phase-resolved wave surface reconstruction using neural networks based on the U-Net and Fourier neural operator (FNO) architectures. Our approach utilizes synthetic yet highly realistic training data on uniform one-dimensional grids, that is generated by the high-order spectral method for wave simulation and a geometric radar modeling approach. The investigation reveals that both models deliver accurate wave reconstruction results and show good generalization for different sea states when trained with spatio-temporal radar data containing multiple historic radar snapshots in each input. Notably, the FNO-based network performs better in handling the data structure imposed by wave physics due to its global approach to learn the mapping between input and desired output in Fourier space.

Surface Similarity Parameter: A New Machine Learning Loss Metric for Oscillatory Spatio-Temporal Data

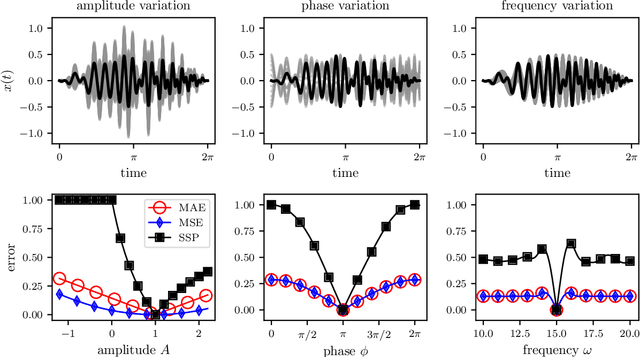
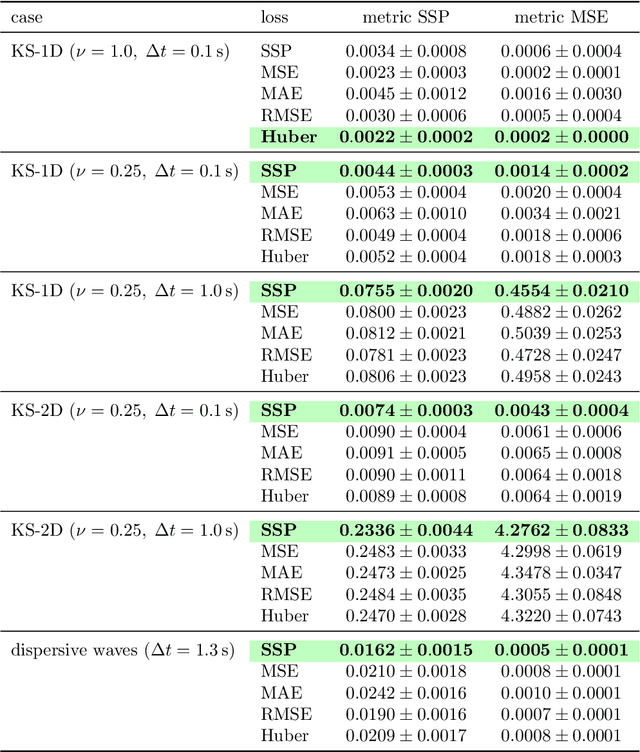
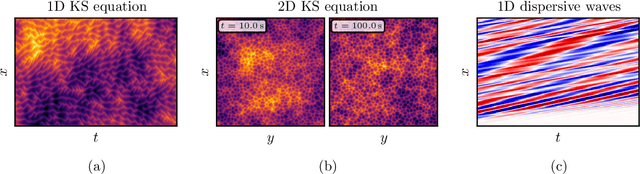
Supervised machine learning approaches require the formulation of a loss functional to be minimized in the training phase. Sequential data are ubiquitous across many fields of research, and are often treated with Euclidean distance-based loss functions that were designed for tabular data. For smooth oscillatory data, those conventional approaches lack the ability to penalize amplitude, frequency and phase prediction errors at the same time, and tend to be biased towards amplitude errors. We introduce the surface similarity parameter (SSP) as a novel loss function that is especially useful for training machine learning models on smooth oscillatory sequences. Our extensive experiments on chaotic spatio-temporal dynamical systems indicate that the SSP is beneficial for shaping gradients, thereby accelerating the training process, reducing the final prediction error, and implementing a stronger regularization effect compared to using classical loss functions. The results indicate the potential of the novel loss metric particularly for highly complex and chaotic data, such as data stemming from the nonlinear two-dimensional Kuramoto-Sivashinsky equation and the linear propagation of dispersive surface gravity waves in fluids.