The First AI4TSP Competition: Learning to Solve Stochastic Routing Problems

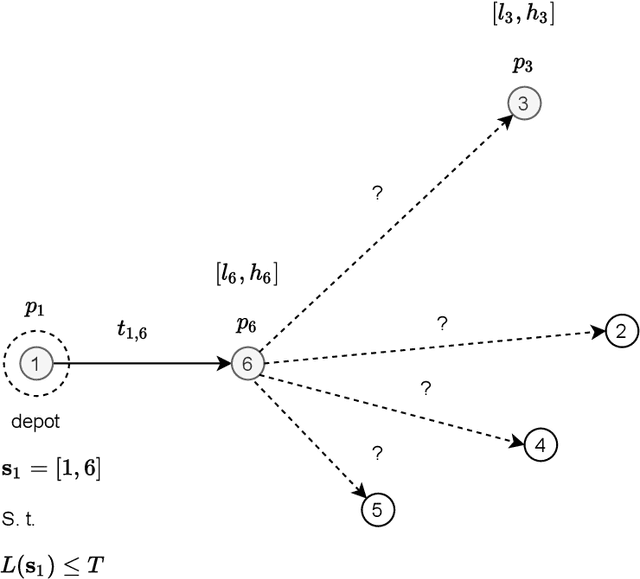
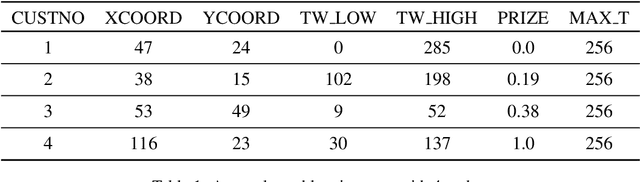
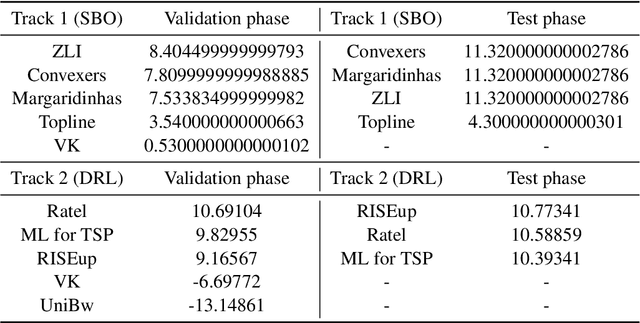
This paper reports on the first international competition on AI for the traveling salesman problem (TSP) at the International Joint Conference on Artificial Intelligence 2021 (IJCAI-21). The TSP is one of the classical combinatorial optimization problems, with many variants inspired by real-world applications. This first competition asked the participants to develop algorithms to solve a time-dependent orienteering problem with stochastic weights and time windows (TD-OPSWTW). It focused on two types of learning approaches: surrogate-based optimization and deep reinforcement learning. In this paper, we describe the problem, the setup of the competition, the winning methods, and give an overview of the results. The winning methods described in this work have advanced the state-of-the-art in using AI for stochastic routing problems. Overall, by organizing this competition we have introduced routing problems as an interesting problem setting for AI researchers. The simulator of the problem has been made open-source and can be used by other researchers as a benchmark for new AI methods.

Learning How to Optimize Black-Box Functions With Extreme Limits on the Number of Function Evaluations

We consider black-box optimization in which only an extremely limited number of function evaluations, on the order of around 100, are affordable and the function evaluations must be performed in even fewer batches of a limited number of parallel trials. This is a typical scenario when optimizing variable settings that are very costly to evaluate, for example in the context of simulation-based optimization or machine learning hyperparameterization. We propose an original method that uses established approaches to propose a set of points for each batch and then down-selects from these candidate points to the number of trials that can be run in parallel. The key novelty of our approach lies in the introduction of a hyperparameterized method for down-selecting the number of candidates to the allowed batch-size, which is optimized offline using automated algorithm configuration. We tune this method for black box optimization and then evaluate on classical black box optimization benchmarks. Our results show that it is possible to learn how to combine evaluation points suggested by highly diverse black box optimization methods conditioned on the progress of the optimization. Compared with the state of the art in black box minimization and various other methods specifically geared towards few-shot minimization, we achieve an average reduction of 50\% of normalized cost, which is a highly significant improvement in performance.

Cost-sensitive Hierarchical Clustering for Dynamic Classifier Selection

We consider the dynamic classifier selection (DCS) problem: Given an ensemble of classifiers, we are to choose which classifier to use depending on the particular input vector that we get to classify. The problem is a special case of the general algorithm selection problem where we have multiple different algorithms we can employ to process a given input. We investigate if a method developed for general algorithm selection named cost-sensitive hierarchical clustering (CSHC) is suited for DCS. We introduce some additions to the original CSHC method for the special case of choosing a classification algorithm and evaluate their impact on performance. We then compare with a number of state-of-the-art dynamic classifier selection methods. Our experimental results show that our modified CSHC algorithm compares favorably