Maximilian Weininger
Solving Robust Markov Decision Processes: Generic, Reliable, Efficient
Dec 13, 2024Abstract:Markov decision processes (MDP) are a well-established model for sequential decision-making in the presence of probabilities. In robust MDP (RMDP), every action is associated with an uncertainty set of probability distributions, modelling that transition probabilities are not known precisely. Based on the known theoretical connection to stochastic games, we provide a framework for solving RMDPs that is generic, reliable, and efficient. It is *generic* both with respect to the model, allowing for a wide range of uncertainty sets, including but not limited to intervals, $L^1$- or $L^2$-balls, and polytopes; and with respect to the objective, including long-run average reward, undiscounted total reward, and stochastic shortest path. It is *reliable*, as our approach not only converges in the limit, but provides precision guarantees at any time during the computation. It is *efficient* because -- in contrast to state-of-the-art approaches -- it avoids explicitly constructing the underlying stochastic game. Consequently, our prototype implementation outperforms existing tools by several orders of magnitude and can solve RMDPs with a million states in under a minute.
1-2-3-Go! Policy Synthesis for Parameterized Markov Decision Processes via Decision-Tree Learning and Generalization
Oct 23, 2024Abstract:Despite the advances in probabilistic model checking, the scalability of the verification methods remains limited. In particular, the state space often becomes extremely large when instantiating parameterized Markov decision processes (MDPs) even with moderate values. Synthesizing policies for such \emph{huge} MDPs is beyond the reach of available tools. We propose a learning-based approach to obtain a reasonable policy for such huge MDPs. The idea is to generalize optimal policies obtained by model-checking small instances to larger ones using decision-tree learning. Consequently, our method bypasses the need for explicit state-space exploration of large models, providing a practical solution to the state-space explosion problem. We demonstrate the efficacy of our approach by performing extensive experimentation on the relevant models from the quantitative verification benchmark set. The experimental results indicate that our policies perform well, even when the size of the model is orders of magnitude beyond the reach of state-of-the-art analysis tools.
Playing Games with your PET: Extending the Partial Exploration Tool to Stochastic Games
May 06, 2024



Abstract:We present version 2.0 of the Partial Exploration Tool (PET), a tool for verification of probabilistic systems. We extend the previous version by adding support for stochastic games, based on a recent unified framework for sound value iteration algorithms. Thereby, PET2 is the first tool implementing a sound and efficient approach for solving stochastic games with objectives of the type reachability/safety and mean payoff. We complement this approach by developing and implementing a partial-exploration based variant for all three objectives. Our experimental evaluation shows that PET2 offers the most efficient partial-exploration based algorithm and is the most viable tool on SGs, even outperforming unsound tools.
What Are the Odds? Improving the foundations of Statistical Model Checking
Apr 08, 2024



Abstract:Markov decision processes (MDPs) are a fundamental model for decision making under uncertainty. They exhibit non-deterministic choice as well as probabilistic uncertainty. Traditionally, verification algorithms assume exact knowledge of the probabilities that govern the behaviour of an MDP. As this assumption is often unrealistic in practice, statistical model checking (SMC) was developed in the past two decades. It allows to analyse MDPs with unknown transition probabilities and provide probably approximately correct (PAC) guarantees on the result. Model-based SMC algorithms sample the MDP and build a model of it by estimating all transition probabilities, essentially for every transition answering the question: ``What are the odds?'' However, so far the statistical methods employed by the state of the art SMC algorithms are quite naive. Our contribution are several fundamental improvements to those methods: On the one hand, we survey statistics literature for better concentration inequalities; on the other hand, we propose specialised approaches that exploit our knowledge of the MDP. Our improvements are generally applicable to many kinds of problem statements because they are largely independent of the setting. Moreover, our experimental evaluation shows that they lead to significant gains, reducing the number of samples that the SMC algorithm has to collect by up to two orders of magnitude.
Stopping Criteria for Value Iteration on Stochastic Games with Quantitative Objectives
Apr 19, 2023



Abstract:A classic solution technique for Markov decision processes (MDP) and stochastic games (SG) is value iteration (VI). Due to its good practical performance, this approximative approach is typically preferred over exact techniques, even though no practical bounds on the imprecision of the result could be given until recently. As a consequence, even the most used model checkers could return arbitrarily wrong results. Over the past decade, different works derived stopping criteria, indicating when the precision reaches the desired level, for various settings, in particular MDP with reachability, total reward, and mean payoff, and SG with reachability. In this paper, we provide the first stopping criteria for VI on SG with total reward and mean payoff, yielding the first anytime algorithms in these settings. To this end, we provide the solution in two flavours: First through a reduction to the MDP case and second directly on SG. The former is simpler and automatically utilizes any advances on MDP. The latter allows for more local computations, heading towards better practical efficiency. Our solution unifies the previously mentioned approaches for MDP and SG and their underlying ideas. To achieve this, we isolate objective-specific subroutines as well as identify objective-independent concepts. These structural concepts, while surprisingly simple, form the very essence of the unified solution.
Algebraically Explainable Controllers: Decision Trees and Support Vector Machines Join Forces
Aug 29, 2022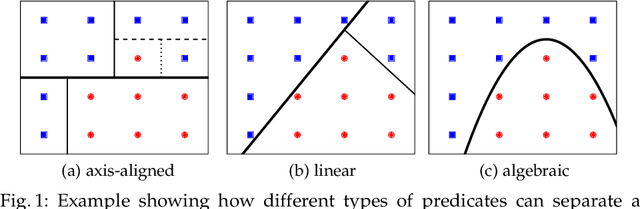

Abstract:Recently, decision trees (DT) have been used as an explainable representation of controllers (a.k.a. strategies, policies, schedulers). Although they are often very efficient and produce small and understandable controllers for discrete systems, complex continuous dynamics still pose a challenge. In particular, when the relationships between variables take more complex forms, such as polynomials, they cannot be obtained using the available DT learning procedures. In contrast, support vector machines provide a more powerful representation, capable of discovering many such relationships, but not in an explainable form. Therefore, we suggest to combine the two frameworks in order to obtain an understandable representation over richer, domain-relevant algebraic predicates. We demonstrate and evaluate the proposed method experimentally on established benchmarks.
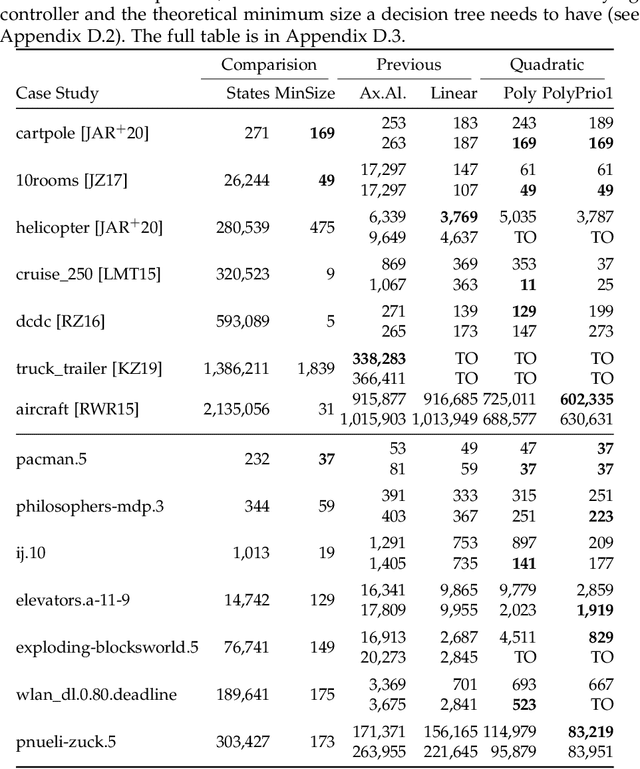
dtControl 2.0: Explainable Strategy Representation via Decision Tree Learning Steered by Experts
Jan 15, 2021
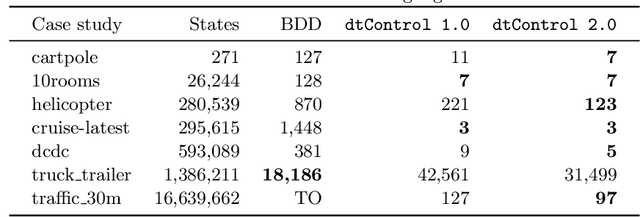
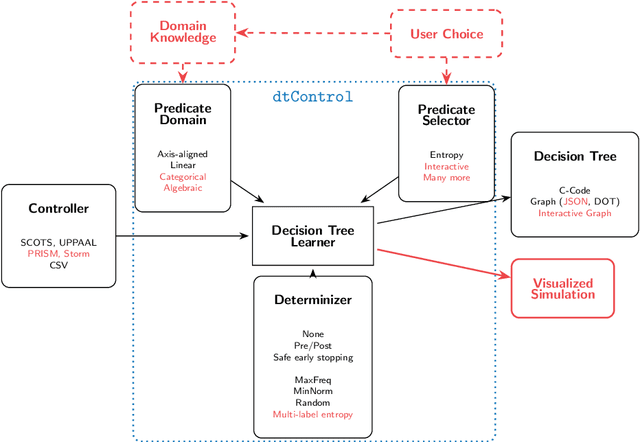
Abstract:Recent advances have shown how decision trees are apt data structures for concisely representing strategies (or controllers) satisfying various objectives. Moreover, they also make the strategy more explainable. The recent tool dtControl had provided pipelines with tools supporting strategy synthesis for hybrid systems, such as SCOTS and Uppaal Stratego. We present dtControl 2.0, a new version with several fundamentally novel features. Most importantly, the user can now provide domain knowledge to be exploited in the decision tree learning process and can also interactively steer the process based on the dynamically provided information. To this end, we also provide a graphical user interface. It allows for inspection and re-computation of parts of the result, suggesting as well as receiving advice on predicates, and visual simulation of the decision-making process. Besides, we interface model checkers of probabilistic systems, namely Storm and PRISM and provide dedicated support for categorical enumeration-type state variables. Consequently, the controllers are more explainable and smaller.
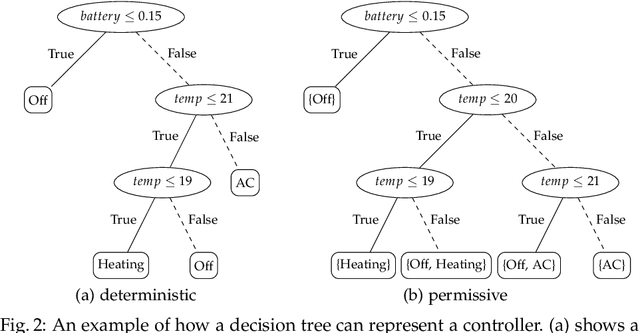
dtControl: Decision Tree Learning Algorithms for Controller Representation
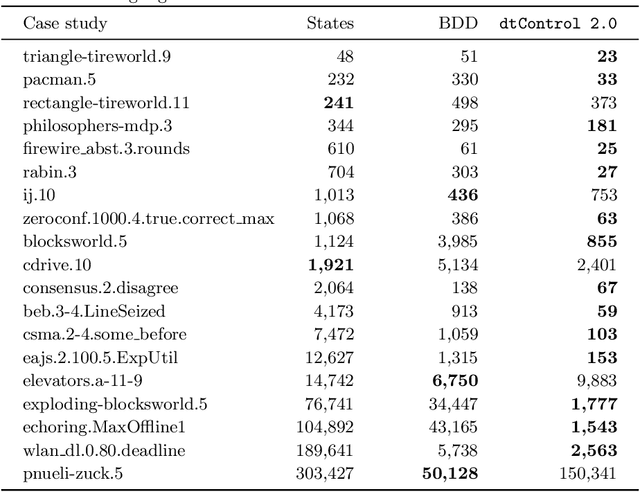
Feb 12, 2020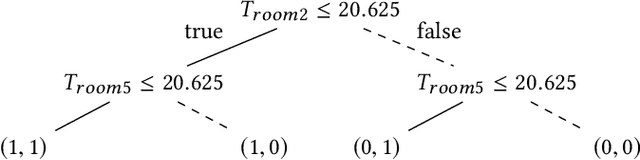
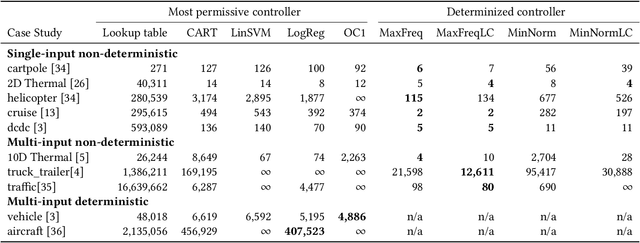

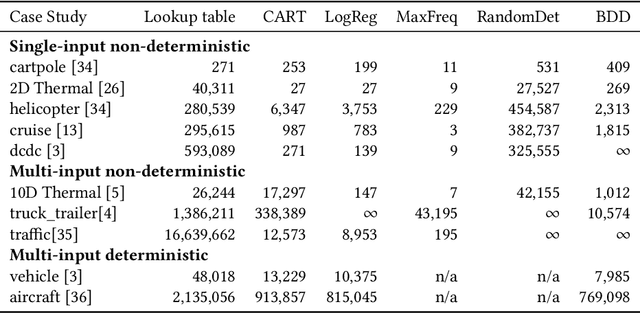
Abstract:Decision tree learning is a popular classification technique most commonly used in machine learning applications. Recent work has shown that decision trees can be used to represent provably-correct controllers concisely. Compared to representations using lookup tables or binary decision diagrams, decision trees are smaller and more explainable. We present dtControl, an easily extensible tool for representing memoryless controllers as decision trees. We give a comprehensive evaluation of various decision tree learning algorithms applied to 10 case studies arising out of correct-by-construction controller synthesis. These algorithms include two new techniques, one for using arbitrary linear binary classifiers in the decision tree learning, and one novel approach for determinizing controllers during the decision tree construction. In particular the latter turns out to be extremely efficient, yielding decision trees with a single-digit number of decision nodes on 5 of the case studies.
PAC Statistical Model Checking for Markov Decision Processes and Stochastic Games
May 24, 2019



Abstract:Statistical model checking (SMC) is a technique for analysis of probabilistic systems that may be (partially) unknown. We present an SMC algorithm for (unbounded) reachability yielding probably approximately correct (PAC) guarantees on the results. We consider both the setting (i) with no knowledge of the transition function (with the only quantity required a bound on the minimum transition probability) and (ii) with knowledge of the topology of the underlying graph. On the one hand, it is the first algorithm for stochastic games. On the other hand, it is the first practical algorithm even for Markov decision processes. Compared to previous approaches where PAC guarantees require running times longer than the age of universe even for systems with a handful of states, our algorithm often yields reasonably precise results within minutes, not requiring the knowledge of mixing time or the topology of the whole model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge