A Self-Improving Coding Agent

We demonstrate that an LLM coding agent, equipped with basic coding tools, can autonomously edit itself, and thereby improve its performance on benchmark tasks. We find performance gains from 17% to 53% on a random subset of SWE Bench Verified, with additional performance gains on LiveCodeBench, as well as synthetically generated agent benchmarks. Our work represents an advancement in the automated and open-ended design of agentic systems, and provides a reference agent framework for those seeking to post-train LLMs on tool use and other agentic tasks.

Bayesian Reward Models for LLM Alignment

To ensure that large language model (LLM) responses are helpful and non-toxic, we usually fine-tune a reward model on human preference data. We then select policy responses with high rewards (best-of-n sampling) or further optimize the policy to produce responses with high rewards (reinforcement learning from human feedback). However, this process is vulnerable to reward overoptimization or hacking, in which the responses selected have high rewards due to errors in the reward model rather than a genuine preference. This is especially problematic as the prompt or response diverges from the training data. It should be possible to mitigate these issues by training a Bayesian reward model, which signals higher uncertainty further from the training data distribution. Therefore, we trained Bayesian reward models using Laplace-LoRA (Yang et al., 2024) and found that the resulting uncertainty estimates can successfully mitigate reward overoptimization in best-of-n sampling.

Bayesian low-rank adaptation for large language models

Parameter-efficient fine-tuning (PEFT) has emerged as a new paradigm for cost-efficient fine-tuning of large language models (LLMs), with low-rank adaptation (LoRA) being a widely adopted choice. However, fine-tuned LLMs often become overconfident especially when fine-tuned on small datasets. Bayesian methods, with their inherent ability to estimate uncertainty, serve as potent tools to mitigate overconfidence and enhance calibration. In this work, we introduce Laplace-LoRA, a straightforward yet effective Bayesian method, which applies the Laplace approximation to the LoRA parameters and, considerably boosts the calibration of fine-tuned LLMs.

Taylor TD-learning

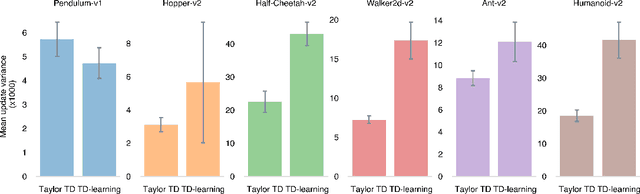
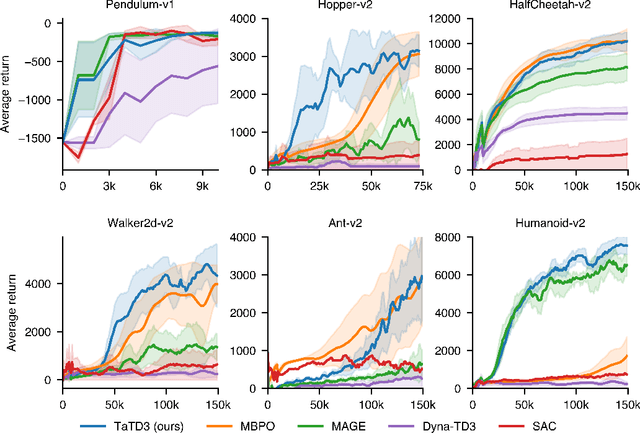
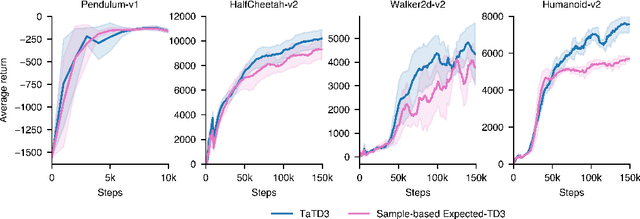
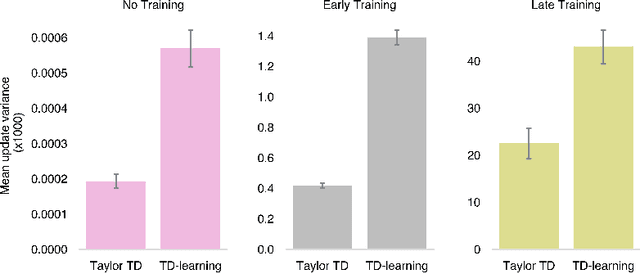
Many reinforcement learning approaches rely on temporal-difference (TD) learning to learn a critic. However, TD-learning updates can be high variance due to their sole reliance on Monte Carlo estimates of the updates. Here, we introduce a model-based RL framework, Taylor TD, which reduces this variance. Taylor TD uses a first-order Taylor series expansion of TD updates. This expansion allows to analytically integrate over stochasticity in the action-choice, and some stochasticity in the state distribution for the initial state and action of each TD update. We include theoretical and empirical evidence of Taylor TD updates being lower variance than (standard) TD updates. Additionally, we show that Taylor TD has the same stable learning guarantees as (standard) TD-learning under linear function approximation. Next, we combine Taylor TD with the TD3 algorithm (Fujimoto et al., 2018), into TaTD3. We show TaTD3 performs as well, if not better, than several state-of-the art model-free and model-based baseline algorithms on a set of standard benchmark tasks. Finally, we include further analysis of the settings in which Taylor TD may be most beneficial to performance relative to standard TD-learning.