Balance Regularized Neural Network Models for Causal Effect Estimation

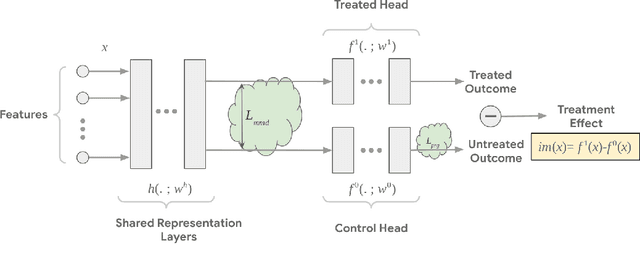
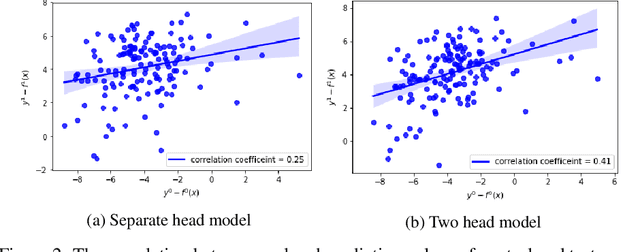
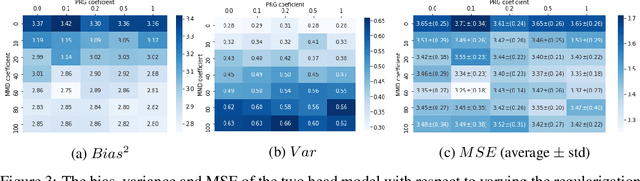
Estimating individual and average treatment effects from observational data is an important problem in many domains such as healthcare and e-commerce. In this paper, we advocate balance regularization of multi-head neural network architectures. Our work is motivated by representation learning techniques to reduce differences between treated and untreated distributions that potentially arise due to confounding factors. We further regularize the model by encouraging it to predict control outcomes for individuals in the treatment group that are similar to control outcomes in the control group. We empirically study the bias-variance trade-off between different weightings of the regularizers, as well as between inductive and transductive inference.

Amortized learning of neural causal representations

Causal models can compactly and efficiently encode the data-generating process under all interventions and hence may generalize better under changes in distribution. These models are often represented as Bayesian networks and learning them scales poorly with the number of variables. Moreover, these approaches cannot leverage previously learned knowledge to help with learning new causal models. In order to tackle these challenges, we represent a novel algorithm called \textit{causal relational networks} (CRN) for learning causal models using neural networks. The CRN represent causal models using continuous representations and hence could scale much better with the number of variables. These models also take in previously learned information to facilitate learning of new causal models. Finally, we propose a decoding-based metric to evaluate causal models with continuous representations. We test our method on synthetic data achieving high accuracy and quick adaptation to previously unseen causal models.

Markov Random Walk Representations with Continuous Distributions

Representations based on random walks can exploit discrete data distributions for clustering and classification. We extend such representations from discrete to continuous distributions. Transition probabilities are now calculated using a diffusion equation with a diffusion coefficient that inversely depends on the data density. We relate this diffusion equation to a path integral and derive the corresponding path probability measure. The framework is useful for incorporating continuous data densities and prior knowledge.