Axiomatic Explainer Globalness via Optimal Transport

Explainability methods are often challenging to evaluate and compare. With a multitude of explainers available, practitioners must often compare and select explainers based on quantitative evaluation metrics. One particular differentiator between explainers is the diversity of explanations for a given dataset; i.e. whether all explanations are identical, unique and uniformly distributed, or somewhere between these two extremes. In this work, we define a complexity measure for explainers, globalness, which enables deeper understanding of the distribution of explanations produced by feature attribution and feature selection methods for a given dataset. We establish the axiomatic properties that any such measure should possess and prove that our proposed measure, Wasserstein Globalness, meets these criteria. We validate the utility of Wasserstein Globalness using image, tabular, and synthetic datasets, empirically showing that it both facilitates meaningful comparison between explainers and improves the selection process for explainability methods.

SmoothHess: ReLU Network Feature Interactions via Stein's Lemma

Several recent methods for interpretability model feature interactions by looking at the Hessian of a neural network. This poses a challenge for ReLU networks, which are piecewise-linear and thus have a zero Hessian almost everywhere. We propose SmoothHess, a method of estimating second-order interactions through Stein's Lemma. In particular, we estimate the Hessian of the network convolved with a Gaussian through an efficient sampling algorithm, requiring only network gradient calls. SmoothHess is applied post-hoc, requires no modifications to the ReLU network architecture, and the extent of smoothing can be controlled explicitly. We provide a non-asymptotic bound on the sample complexity of our estimation procedure. We validate the superior ability of SmoothHess to capture interactions on benchmark datasets and a real-world medical spirometry dataset.

Explanation Uncertainty with Decision Boundary Awareness

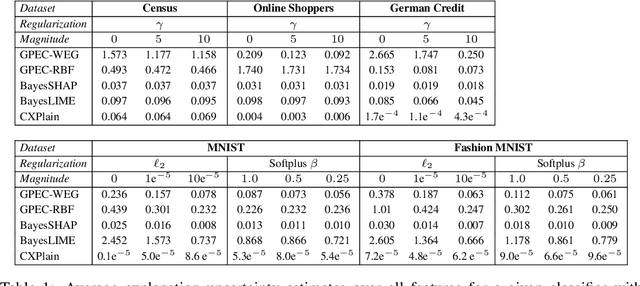
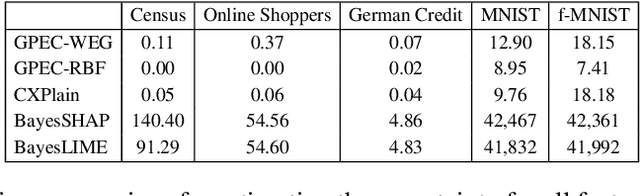
Post-hoc explanation methods have become increasingly depended upon for understanding black-box classifiers in high-stakes applications, precipitating a need for reliable explanations. While numerous explanation methods have been proposed, recent works have shown that many existing methods can be inconsistent or unstable. In addition, high-performing classifiers are often highly nonlinear and can exhibit complex behavior around the decision boundary, leading to brittle or misleading local explanations. Therefore, there is an impending need to quantify the uncertainty of such explanation methods in order to understand when explanations are trustworthy. We introduce a novel uncertainty quantification method parameterized by a Gaussian Process model, which combines the uncertainty approximation of existing methods with a novel geodesic-based similarity which captures the complexity of the target black-box decision boundary. The proposed framework is highly flexible; it can be used with any black-box classifier and feature attribution method to amortize uncertainty estimates for explanations. We show theoretically that our proposed geodesic-based kernel similarity increases with the complexity of the decision boundary. Empirical results on multiple tabular and image datasets show that our decision boundary-aware uncertainty estimate improves understanding of explanations as compared to existing methods.

Unsupervised Approaches for Out-Of-Distribution Dermoscopic Lesion Detection

There are limited works showing the efficacy of unsupervised Out-of-Distribution (OOD) methods on complex medical data. Here, we present preliminary findings of our unsupervised OOD detection algorithm, SimCLR-LOF, as well as a recent state of the art approach (SSD), applied on medical images. SimCLR-LOF learns semantically meaningful features using SimCLR and uses LOF for scoring if a test sample is OOD. We evaluated on the multi-source International Skin Imaging Collaboration (ISIC) 2019 dataset, and show results that are competitive with SSD as well as with recent supervised approaches applied on the same data.