Explanation Uncertainty with Decision Boundary Awareness
Paper and Code
Oct 05, 2022
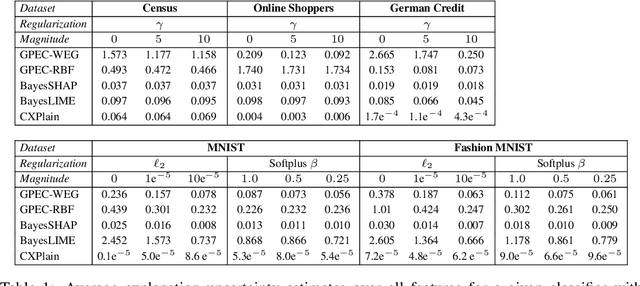

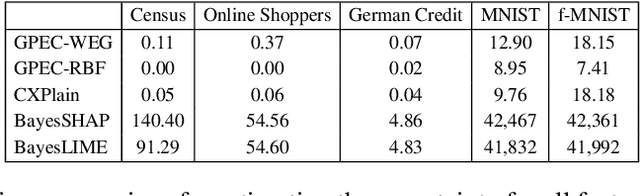
Post-hoc explanation methods have become increasingly depended upon for understanding black-box classifiers in high-stakes applications, precipitating a need for reliable explanations. While numerous explanation methods have been proposed, recent works have shown that many existing methods can be inconsistent or unstable. In addition, high-performing classifiers are often highly nonlinear and can exhibit complex behavior around the decision boundary, leading to brittle or misleading local explanations. Therefore, there is an impending need to quantify the uncertainty of such explanation methods in order to understand when explanations are trustworthy. We introduce a novel uncertainty quantification method parameterized by a Gaussian Process model, which combines the uncertainty approximation of existing methods with a novel geodesic-based similarity which captures the complexity of the target black-box decision boundary. The proposed framework is highly flexible; it can be used with any black-box classifier and feature attribution method to amortize uncertainty estimates for explanations. We show theoretically that our proposed geodesic-based kernel similarity increases with the complexity of the decision boundary. Empirical results on multiple tabular and image datasets show that our decision boundary-aware uncertainty estimate improves understanding of explanations as compared to existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge