Extension-ranking Semantics for Abstract Argumentation Preprint

In this paper, we present a general framework for ranking sets of arguments in abstract argumentation based on their plausibility of acceptance. We present a generalisation of Dung's extension semantics as extension-ranking semantics, which induce a preorder over the power set of all arguments, allowing us to state that one set is "closer" to being acceptable than another. To evaluate the extension-ranking semantics, we introduce a number of principles that a well-behaved extension-ranking semantics should satisfy. We consider several simple base relations, each of which models a single central aspect of argumentative reasoning. The combination of these base relations provides us with a family of extension-ranking semantics. We also adapt a number of approaches from the literature for ranking extensions to be usable in the context of extension-ranking semantics, and evaluate their behaviour.

Reasoning with maximal consistent signatures

We analyse a specific instance of the general approach of reasoning based on forgetting by Lang and Marquis. More precisely, we discuss an approach for reasoning with inconsistent information using maximal consistent subsignatures, where a maximal consistent subsignature is a maximal set of propositions such that forgetting the remaining propositions restores consistency. We analyse maximal consistent subsignatures and the corresponding minimal inconsistent subsignatures in-depth and show, among others, that the hitting set duality applies for them as well. We further analyse inference relations based on maximal consistent subsignatures wrt. rationality postulates from non-monotonic reasoning and computational complexity. We also consider the relationship of our approach with inconsistency measurement and paraconsistent reasoning.

Revisiting Vacuous Reduct Semantics for Abstract Argumentation (Extended Version)

We consider the notion of a vacuous reduct semantics for abstract argumentation frameworks, which, given two abstract argumentation semantics {\sigma} and {\tau}, refines {\sigma} (base condition) by accepting only those {\sigma}-extensions that have no non-empty {\tau}-extension in their reduct (vacuity condition). We give a systematic overview on vacuous reduct semantics resulting from combining different admissibility-based and conflict-free semantics and present a principle-based analysis of vacuous reduct semantics in general. We provide criteria for the inheritance of principle satisfaction by a vacuous reduct semantics from its base and vacuity condition for established as well as recently introduced principles in the context of weak argumentation semantics. We also conduct a principle-based analysis for the special case of undisputed semantics.

The Realizability of Revision and Contraction Operators in Epistemic Spaces

This paper studies the realizability of belief revision and belief contraction operators in epistemic spaces. We observe that AGM revision and AGM contraction operators for epistemic spaces are only realizable in precisely determined epistemic spaces. We define the class of linear change operators, a special kind of maxichoice operator. When AGM revision, respectively, AGM contraction, is realizable, linear change operators are a canonical realization.

Comparison of SAT-based and ASP-based Algorithms for Inconsistency Measurement

We present algorithms based on satisfiability problem (SAT) solving, as well as answer set programming (ASP), for solving the problem of determining inconsistency degrees in propositional knowledge bases. We consider six different inconsistency measures whose respective decision problems lie on the first level of the polynomial hierarchy. Namely, these are the contension inconsistency measure, the forgetting-based inconsistency measure, the hitting set inconsistency measure, the max-distance inconsistency measure, the sum-distance inconsistency measure, and the hit-distance inconsistency measure. In an extensive experimental analysis, we compare the SAT-based and ASP-based approaches with each other, as well as with a set of naive baseline algorithms. Our results demonstrate that overall, both the SAT-based and the ASP-based approaches clearly outperform the naive baseline methods in terms of runtime. The results further show that the proposed ASP-based approaches perform superior to the SAT-based ones with regard to all six inconsistency measures considered in this work. Moreover, we conduct additional experiments to explain the aforementioned results in greater detail.

Measuring Inconsistency in Declarative Process Specifications

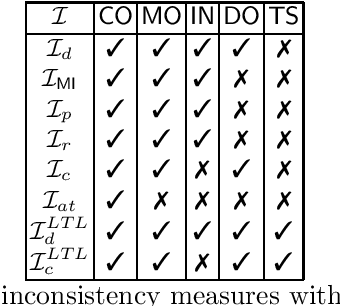
We address the problem of measuring inconsistency in declarative process specifications, with an emphasis on linear temporal logic on fixed traces (LTLff). As we will show, existing inconsistency measures for classical logic cannot provide a meaningful assessment of inconsistency in LTL in general, as they cannot adequately handle the temporal operators. We therefore propose a novel paraconsistent semantics as a framework for inconsistency measurement. We then present two new inconsistency measures based on these semantics and show that they satisfy important desirable properties. We show how these measures can be applied to declarative process models and investigate the computational complexity of the introduced approach.

Revisiting initial sets in abstract argumentation

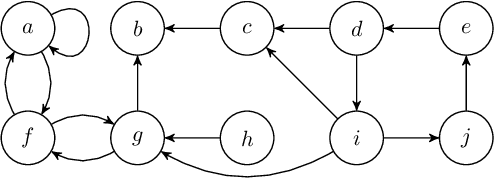
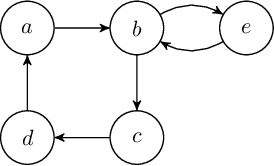
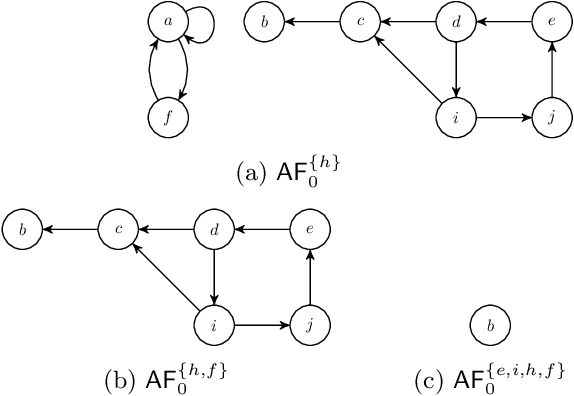
We revisit the notion of initial sets by Xu and Cayrol, i.e., non-empty minimal admissible sets in abstract argumentation frameworks. Initial sets are a simple concept for analysing conflicts in an abstract argumentation framework and to explain why certain arguments can be accepted. We contribute with new insights on the structure of initial sets and devise a simple non-deterministic construction principle for any admissible set, based on iterative selection of initial sets of the original framework and its induced reducts. In particular, we characterise many existing admissibility-based semantics via this construction principle, thus providing a constructive explanation on the structure of extensions. We also investigate certain problems related to initial sets with respect to their computational complexity.

Fudge: A light-weight solver for abstract argumentation based on SAT reductions

We present Fudge, an abstract argumentation solver that tightly integrates satisfiability solving technology to solve a series of abstract argumentation problems. While most of the encodings used by Fudge derive from standard translation approaches, Fudge makes use of completely novel encodings to solve the skeptical reasoning problem wrt. preferred semantics and problems wrt. ideal semantics.

Measuring Inconsistency over Sequences of Business Rule Cases

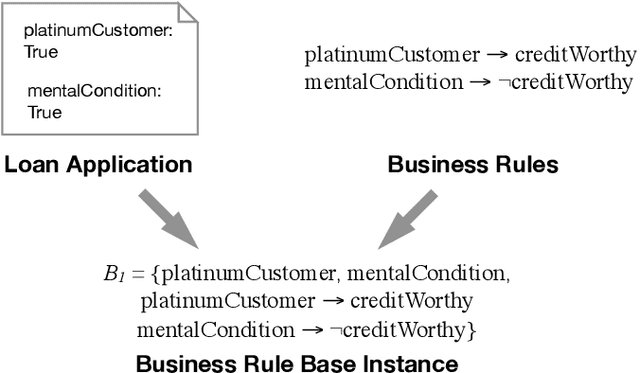
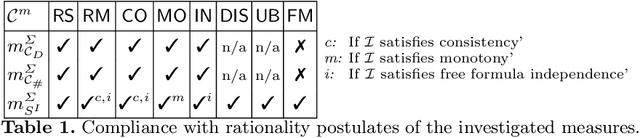
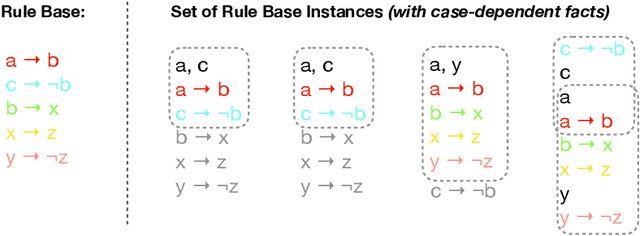
In this report, we investigate (element-based) inconsistency measures for multisets of business rule bases. Currently, related works allow to assess individual rule bases, however, as companies might encounter thousands of such instances daily, studying not only individual rule bases separately, but rather also their interrelations becomes necessary, especially in regard to determining suitable re-modelling strategies. We therefore present an approach to induce multiset-measures from arbitrary (traditional) inconsistency measures, propose new rationality postulates for a multiset use-case, and investigate the complexity of various aspects regarding multi-rule base inconsistency measurement.

Towards Ranking-based Semantics for Abstract Argumentation using Conditional Logic Semantics

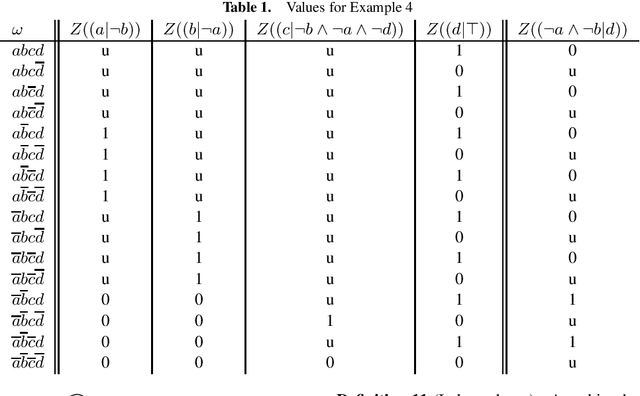
We propose a novel ranking-based semantics for Dung-style argumentation frameworks with the help of conditional logics. Using an intuitive translation for an argumentation framework to generate conditionals, we can apply nonmonotonic inference systems to generate a ranking on possible worlds. With this ranking we construct a ranking for our arguments. With a small extension to this ranking-based semantics we already satisfy some desirable properties for a ranking over arguments.