Revisiting initial sets in abstract argumentation
Paper and Code
Apr 21, 2022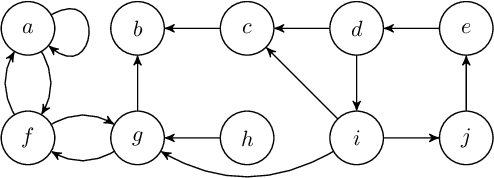

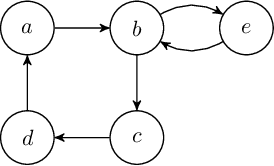
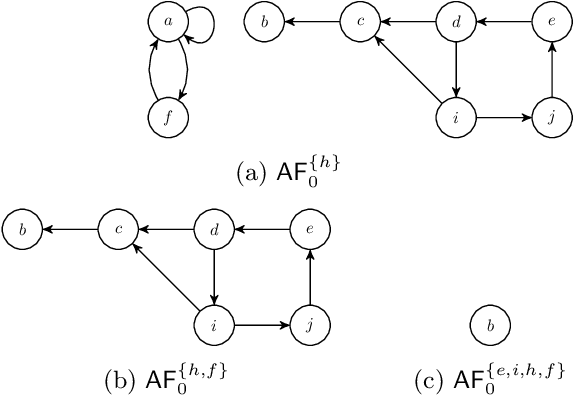
We revisit the notion of initial sets by Xu and Cayrol, i.e., non-empty minimal admissible sets in abstract argumentation frameworks. Initial sets are a simple concept for analysing conflicts in an abstract argumentation framework and to explain why certain arguments can be accepted. We contribute with new insights on the structure of initial sets and devise a simple non-deterministic construction principle for any admissible set, based on iterative selection of initial sets of the original framework and its induced reducts. In particular, we characterise many existing admissibility-based semantics via this construction principle, thus providing a constructive explanation on the structure of extensions. We also investigate certain problems related to initial sets with respect to their computational complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge