Credibility-Limited Revision for Epistemic Spaces

We consider credibility-limited revision in the framework of belief change for epistemic spaces, permitting inconsistent belief sets and inconsistent beliefs. In this unrestricted setting, the class of credibility-limited revision operators does not include any AGM revision operators. We extend the class of credibility-limited revision operators in a way that all AGM revision operators are included while keeping the original spirit of credibility-limited revision. Extended credibility-limited revision operators are defined axiomatically. A semantic characterization of extended credibility-limited revision operators that employ total preorders on possible worlds is presented.

The Realizability of Revision and Contraction Operators in Epistemic Spaces

This paper studies the realizability of belief revision and belief contraction operators in epistemic spaces. We observe that AGM revision and AGM contraction operators for epistemic spaces are only realizable in precisely determined epistemic spaces. We define the class of linear change operators, a special kind of maxichoice operator. When AGM revision, respectively, AGM contraction, is realizable, linear change operators are a canonical realization.

A Primer for Preferential Non-Monotonic Propositional Team Logics

This paper considers KLM-style preferential non-monotonic reasoning in the setting of propositional team semantics. We show that team-based propositional logics naturally give rise to cumulative non-monotonic entailment relations. Motivated by the non-classical interpretation of disjunction in team semantics, we give a precise characterization for preferential models for propositional dependence logic satisfying all of System P postulates. Furthermore, we show how classical entailment and dependence logic entailment can be expressed in terms of non-trivial preferential models.

Iterated Belief Change, Computationally

Iterated Belief Change is the research area that investigates principles for the dynamics of beliefs over (possibly unlimited) many subsequent belief changes. In this paper, we demonstrate how iterated belief change is connected to computation. In particular, we show that iterative belief revision is Turing complete, even under the condition that broadly accepted principles like the Darwiche-Pearl postulates for iterated revision hold.

A Conditional Perspective on the Logic of Iterated Belief Contraction

In this article, we consider iteration principles for contraction, with the goal of identifying properties for contractions that respect conditional beliefs. Therefore, we investigate and evaluate four groups of iteration principles for contraction which consider the dynamics of conditional beliefs. For all these principles, we provide semantic characterization theorems and provide formulations by postulates which highlight how the change of beliefs and of conditional beliefs is constrained, whenever that is possible. The first group is similar to the syntactic Darwiche-Pearl postulates. As a second group, we consider semantic postulates for iteration of contraction by Chopra, Ghose, Meyer and Wong, and by Konieczny and Pino P\'erez, respectively, and we provide novel syntactic counterparts. Third, we propose a contraction analogue of the independence condition by Jin and Thielscher. For the fourth group, we consider natural and moderate contraction by Nayak. Methodically, we make use of conditionals for contractions, so-called contractionals and furthermore, we propose and employ the novel notion of $ \alpha $-equivalence for formulating some of the new postulates.

Semantic Characterizations of General Belief Base Revision

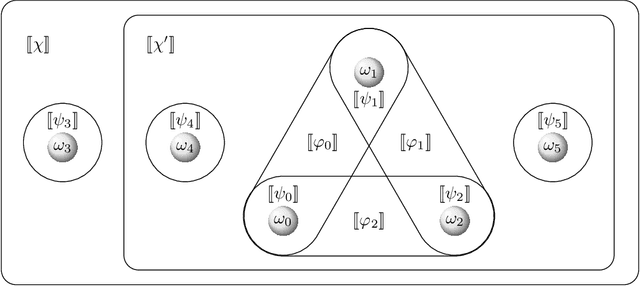
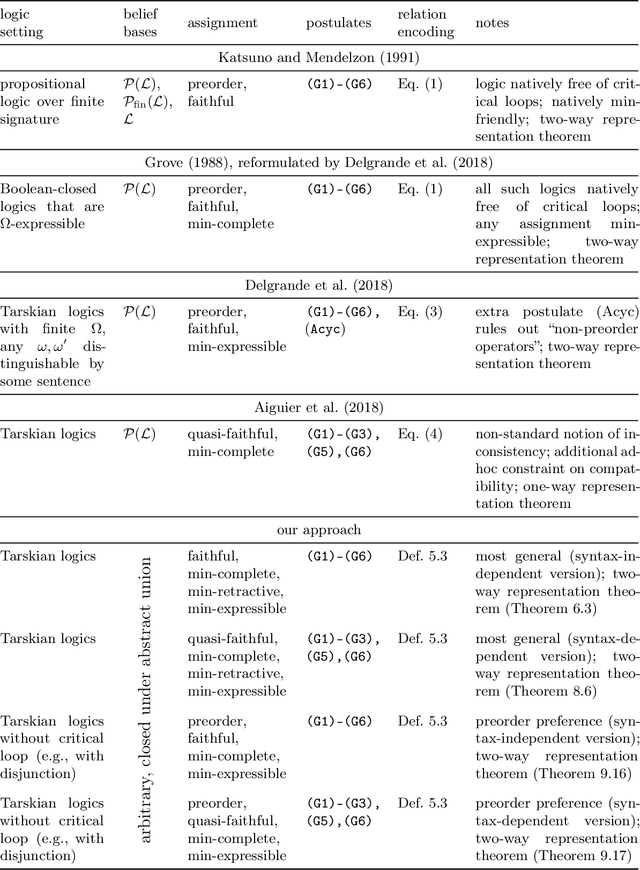
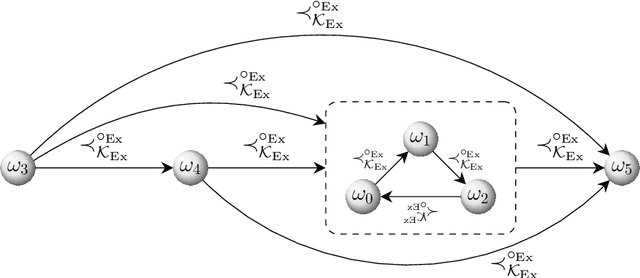
The AGM postulates by Alchourr\'on, G\"ardenfors, and Makinson continue to represent a cornerstone in research related to belief change. Katsuno and Mendelzon (K&M) adopted the AGM postulates for changing belief bases and characterized AGM belief base revision in propositional logic over finite signatures. We generalize K&M's approach to the setting of (multiple) base revision in arbitrary Tarskian logics, covering all logics with a classical model-theoretic semantics and hence a wide variety of logics used in knowledge representation and beyond. Our generic formulation applies to various notions of "base" (such as belief sets, arbitrary or finite sets of sentences, or single sentences). The core result is a representation theorem showing a two-way correspondence between AGM base revision operators and certain "assignments": functions mapping belief bases to total - yet not transitive - "preference" relations between interpretations. Alongside, we present a companion result for the case when the AGM postulate of syntax-independence is abandoned. We also provide a characterization of all logics for which our result can be strengthened to assignments producing transitive preference relations (as in K&M's original work), giving rise to two more representation theorems for such logics, according to syntax dependence vs. independence.

Conditional Inference and Activation of Knowledge Entities in ACT-R

Activation-based conditional inference applies conditional reasoning to ACT-R, a cognitive architecture developed to formalize human reasoning. The idea of activation-based conditional inference is to determine a reasonable subset of a conditional belief base in order to draw inductive inferences in time. Central to activation-based conditional inference is the activation function which assigns to the conditionals in the belief base a degree of activation mainly based on the conditional's relevance for the current query and its usage history. Therewith, our approach integrates several aspects of human reasoning into expert systems such as focusing, forgetting, and remembering.

On Limited Non-Prioritised Belief Revision Operators with Dynamic Scope

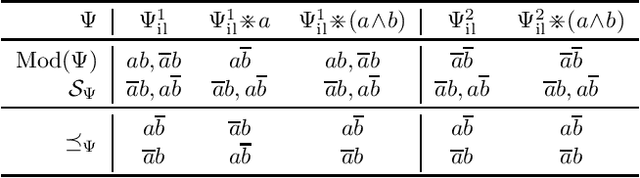
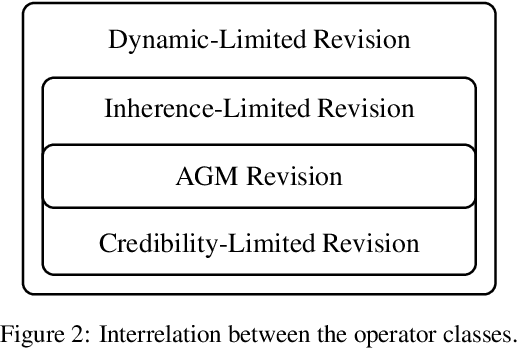
The research on non-prioritized revision studies revision operators which do not accept all new beliefs. In this paper, we contribute to this line of research by introducing the concept of dynamic-limited revision, which are revisions expressible by a total preorder over a limited set of worlds. For a belief change operator, we consider the scope, which consists of those beliefs which yield success of revision. We show that for each set satisfying single sentence closure and disjunction completeness there exists a dynamic-limited revision having the union of this set with the beliefs set as scope. We investigate iteration postulates for belief and scope dynamics and characterise them for dynamic-limited revision. As an application, we employ dynamic-limited revision to studying belief revision in the context of so-called inherent beliefs, which are beliefs globally accepted by the agent. This leads to revision operators which we call inherence-limited. We present a representation theorem for inherence-limited revision, and we compare these operators and dynamic-limited revision with the closely related credible-limited revision operators.

A General Katsuno-Mendelzon-Style Characterization of AGM Belief Base Revision for Arbitrary Monotonic Logics

The AGM postulates by Alchourr\'{o}n, G\"{a}rdenfors, and Makinson continue to represent a cornerstone in research related to belief change. We generalize the approach of Katsuno and Mendelzon (KM) for characterizing AGM base revision from propositional logic to the setting of (multiple) base revision in arbitrary monotonic logics. Our core result is a representation theorem using the assignment of total - yet not transitive - "preference" relations to belief bases. We also provide a characterization of all logics for which our result can be strengthened to preorder assignments (as in KM's original work).

Descriptor Revision for Conditionals: Literal Descriptors and Conditional Preservation

Descriptor revision by Hansson is a framework for addressing the problem of belief change. In descriptor revision, different kinds of change processes are dealt with in a joint framework. Individual change requirements are qualified by specific success conditions expressed by a belief descriptor, and belief descriptors can be combined by logical connectives. This is in contrast to the currently dominating AGM paradigm shaped by Alchourr\'on, G\"ardenfors, and Makinson, where different kinds of changes, like a revision or a contraction, are dealt with separately. In this article, we investigate the realisation of descriptor revision for a conditional logic while restricting descriptors to the conjunction of literal descriptors. We apply the principle of conditional preservation developed by Kern-Isberner to descriptor revision for conditionals, show how descriptor revision for conditionals under these restrictions can be characterised by a constraint satisfaction problem, and implement it using constraint logic programming. Since our conditional logic subsumes propositional logic, our approach also realises descriptor revision for propositional logic.