Semantic Characterizations of General Belief Base Revision

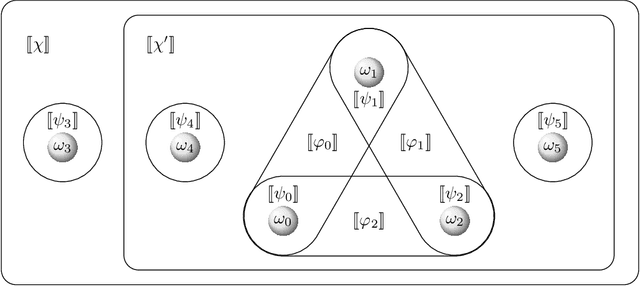
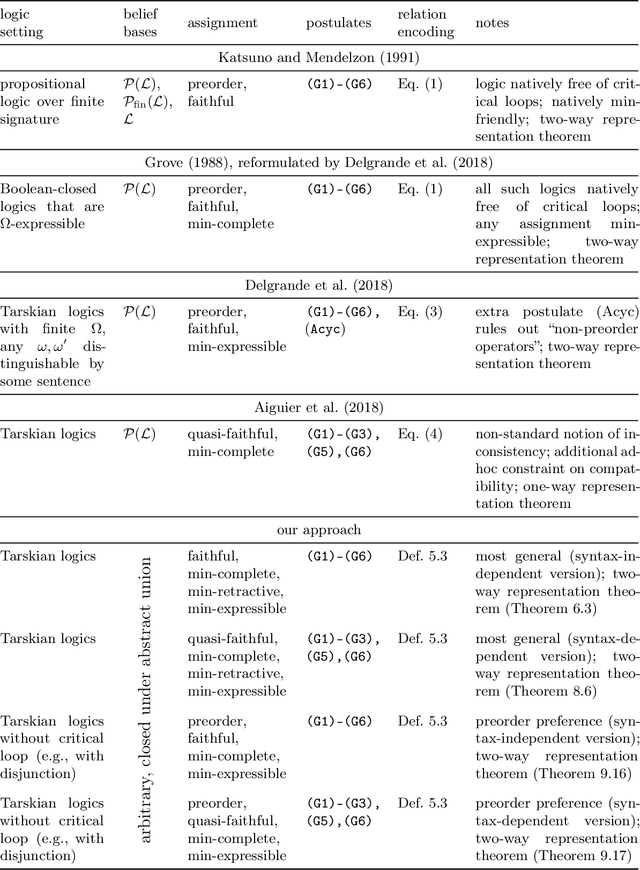
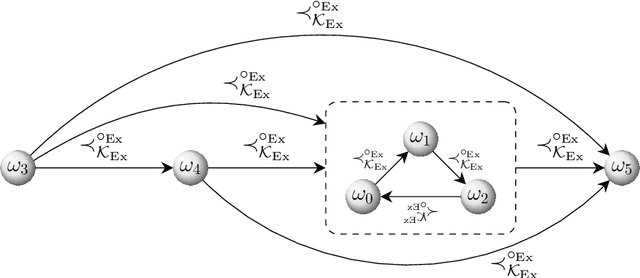
The AGM postulates by Alchourr\'on, G\"ardenfors, and Makinson continue to represent a cornerstone in research related to belief change. Katsuno and Mendelzon (K&M) adopted the AGM postulates for changing belief bases and characterized AGM belief base revision in propositional logic over finite signatures. We generalize K&M's approach to the setting of (multiple) base revision in arbitrary Tarskian logics, covering all logics with a classical model-theoretic semantics and hence a wide variety of logics used in knowledge representation and beyond. Our generic formulation applies to various notions of "base" (such as belief sets, arbitrary or finite sets of sentences, or single sentences). The core result is a representation theorem showing a two-way correspondence between AGM base revision operators and certain "assignments": functions mapping belief bases to total - yet not transitive - "preference" relations between interpretations. Alongside, we present a companion result for the case when the AGM postulate of syntax-independence is abandoned. We also provide a characterization of all logics for which our result can be strengthened to assignments producing transitive preference relations (as in K&M's original work), giving rise to two more representation theorems for such logics, according to syntax dependence vs. independence.

A General Katsuno-Mendelzon-Style Characterization of AGM Belief Base Revision for Arbitrary Monotonic Logics

The AGM postulates by Alchourr\'{o}n, G\"{a}rdenfors, and Makinson continue to represent a cornerstone in research related to belief change. We generalize the approach of Katsuno and Mendelzon (KM) for characterizing AGM base revision from propositional logic to the setting of (multiple) base revision in arbitrary monotonic logics. Our core result is a representation theorem using the assignment of total - yet not transitive - "preference" relations to belief bases. We also provide a characterization of all logics for which our result can be strengthened to preorder assignments (as in KM's original work).