Gabriele Kern-Isberner
Extension-ranking Semantics for Abstract Argumentation Preprint
Apr 30, 2025Abstract:In this paper, we present a general framework for ranking sets of arguments in abstract argumentation based on their plausibility of acceptance. We present a generalisation of Dung's extension semantics as extension-ranking semantics, which induce a preorder over the power set of all arguments, allowing us to state that one set is "closer" to being acceptable than another. To evaluate the extension-ranking semantics, we introduce a number of principles that a well-behaved extension-ranking semantics should satisfy. We consider several simple base relations, each of which models a single central aspect of argumentative reasoning. The combination of these base relations provides us with a family of extension-ranking semantics. We also adapt a number of approaches from the literature for ranking extensions to be usable in the context of extension-ranking semantics, and evaluate their behaviour.
On Establishing Robust Consistency in Answer Set Programs
Aug 17, 2022



Abstract:Answer set programs used in real-world applications often require that the program is usable with different input data. This, however, can often lead to contradictory statements and consequently to an inconsistent program. Causes for potential contradictions in a program are conflicting rules. In this paper, we show how to ensure that a program $\mathcal{P}$ remains non-contradictory given any allowed set of such input data. For that, we introduce the notion of conflict-resolving $\lambda$- extensions. A conflict-resolving $\lambda$-extension for a conflicting rule $r$ is a set $\lambda$ of (default) literals such that extending the body of $r$ by $\lambda$ resolves all conflicts of $r$ at once. We investigate the properties that suitable $\lambda$-extensions should possess and building on that, we develop a strategy to compute all such conflict-resolving $\lambda$-extensions for each conflicting rule in $\mathcal{P}$. We show that by implementing a conflict resolution process that successively resolves conflicts using $\lambda$-extensions eventually yields a program that remains non-contradictory given any allowed set of input data.
A Conditional Perspective on the Logic of Iterated Belief Contraction
Feb 04, 2022



Abstract:In this article, we consider iteration principles for contraction, with the goal of identifying properties for contractions that respect conditional beliefs. Therefore, we investigate and evaluate four groups of iteration principles for contraction which consider the dynamics of conditional beliefs. For all these principles, we provide semantic characterization theorems and provide formulations by postulates which highlight how the change of beliefs and of conditional beliefs is constrained, whenever that is possible. The first group is similar to the syntactic Darwiche-Pearl postulates. As a second group, we consider semantic postulates for iteration of contraction by Chopra, Ghose, Meyer and Wong, and by Konieczny and Pino P\'erez, respectively, and we provide novel syntactic counterparts. Third, we propose a contraction analogue of the independence condition by Jin and Thielscher. For the fourth group, we consider natural and moderate contraction by Nayak. Methodically, we make use of conditionals for contractions, so-called contractionals and furthermore, we propose and employ the novel notion of $ \alpha $-equivalence for formulating some of the new postulates.
Conditional Inference and Activation of Knowledge Entities in ACT-R
Oct 28, 2021



Abstract:Activation-based conditional inference applies conditional reasoning to ACT-R, a cognitive architecture developed to formalize human reasoning. The idea of activation-based conditional inference is to determine a reasonable subset of a conditional belief base in order to draw inductive inferences in time. Central to activation-based conditional inference is the activation function which assigns to the conditionals in the belief base a degree of activation mainly based on the conditional's relevance for the current query and its usage history. Therewith, our approach integrates several aspects of human reasoning into expert systems such as focusing, forgetting, and remembering.
On Limited Non-Prioritised Belief Revision Operators with Dynamic Scope
Aug 17, 2021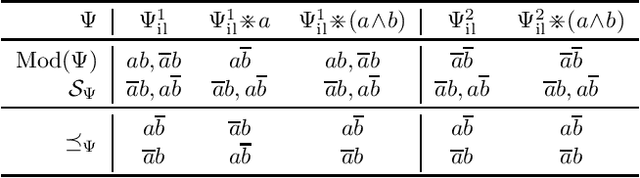
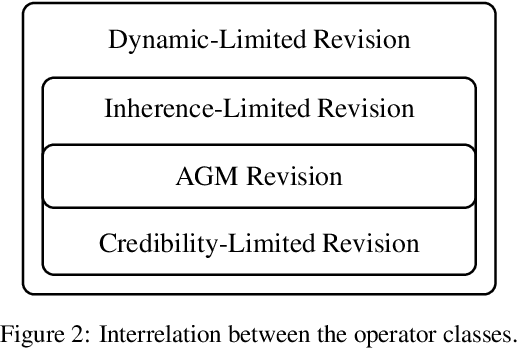
Abstract:The research on non-prioritized revision studies revision operators which do not accept all new beliefs. In this paper, we contribute to this line of research by introducing the concept of dynamic-limited revision, which are revisions expressible by a total preorder over a limited set of worlds. For a belief change operator, we consider the scope, which consists of those beliefs which yield success of revision. We show that for each set satisfying single sentence closure and disjunction completeness there exists a dynamic-limited revision having the union of this set with the beliefs set as scope. We investigate iteration postulates for belief and scope dynamics and characterise them for dynamic-limited revision. As an application, we employ dynamic-limited revision to studying belief revision in the context of so-called inherent beliefs, which are beliefs globally accepted by the agent. This leads to revision operators which we call inherence-limited. We present a representation theorem for inherence-limited revision, and we compare these operators and dynamic-limited revision with the closely related credible-limited revision operators.
A Conditional Perspective for Iterated Belief Contraction
Nov 20, 2019

Abstract:According to Boutillier, Darwiche, Pearl and others, principles for iterated revision can be characterised in terms of changing beliefs about conditionals. For iterated contraction a similar formulation is not known. This is especially because for iterated belief change the connection between revision and contraction via the Levi and Harper identity is not straightforward, and therefore, characterisation results do not transfer easily between iterated revision and contraction. In this article, we develop an axiomatisation of iterated contraction in terms of changing conditional beliefs. We prove that the new set of postulates conforms semantically to the class of operators like the ones given by Konieczny and Pino P\'erez for iterated contraction.
Stratified Labelings for Abstract Argumentation
Aug 04, 2013



Abstract:We introduce stratified labelings as a novel semantical approach to abstract argumentation frameworks. Compared to standard labelings, stratified labelings provide a more fine-grained assessment of the controversiality of arguments using ranks instead of the usual labels in, out, and undecided. We relate the framework of stratified labelings to conditional logic and, in particular, to the System Z ranking functions.
A Constraint Logic Programming Approach for Computing Ordinal Conditional Functions
Aug 30, 2011

Abstract:In order to give appropriate semantics to qualitative conditionals of the form "if A then normally B", ordinal conditional functions (OCFs) ranking the possible worlds according to their degree of plausibility can be used. An OCF accepting all conditionals of a knowledge base R can be characterized as the solution of a constraint satisfaction problem. We present a high-level, declarative approach using constraint logic programming techniques for solving this constraint satisfaction problem. In particular, the approach developed here supports the generation of all minimal solutions; these minimal solutions are of special interest as they provide a basis for model-based inference from R.
Conditional indifference and conditional preservation
Mar 06, 2000



Abstract:The idea of preserving conditional beliefs emerged recently as a new paradigm apt to guide the revision of epistemic states. Conditionals are substantially different from propositional beliefs and need specific treatment. In this paper, we present a new approach to conditionals, capturing particularly well their dynamic part as revision policies. We thoroughly axiomatize a principle of conditional preservation as an indifference property with respect to conditional structures of worlds. This principle is developed in a semi-quantitative setting, so as to reveal its fundamental meaning for belief revision in quantitative as well as in qualitative frameworks. In fact, it is shown to cover other proposed approaches to conditional preservation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge