Finite Compressive Sensing

This paper introduces a sparse projection matrix composed of discrete (digital) periodic lines that create a pseudo-random (p.frac) sampling scheme. Our approach enables random Cartesian sampling whilst employing deterministic and one-dimensional (1D) trajectories derived from the discrete Radon transform (DRT). Unlike radial trajectories, DRT projections can be back-projected without interpolation. Thus, we also propose a novel reconstruction method based on the exact projections of the DRT called finite Fourier reconstruction (FFR). We term this combined p.frac and FFR strategy Finite Compressive Sensing (FCS), with image recovery demonstrated on experimental and simulated data; image quality comparisons are made with Cartesian random sampling in 1D and two-dimensional (2D), as well as radial under-sampling in a more constrained experiment. Our experiments indicate FCS enables 3-5dB gain in peak signal-to-noise ratio (PSNR) for 2-, 4- and 8-fold under-sampling compared to 1D Cartesian random sampling. This paper aims to: Review common sampling strategies for compressed sensing (CS)-magnetic resonance imaging (MRI) to inform the motivation of a projective and Cartesian sampling scheme. Compare the incoherence of these sampling strategies and the proposed p.frac. Compare reconstruction quality of the sampling schemes under various reconstruction strategies to determine the suitability of p.frac for CS-MRI. It is hypothesised that because p.frac is a highly incoherent sampling scheme, that reconstructions will be of high quality compared to 1D Cartesian phase-encode under-sampling.

CAN3D: Fast 3D Medical Image Segmentation via Compact Context Aggregation

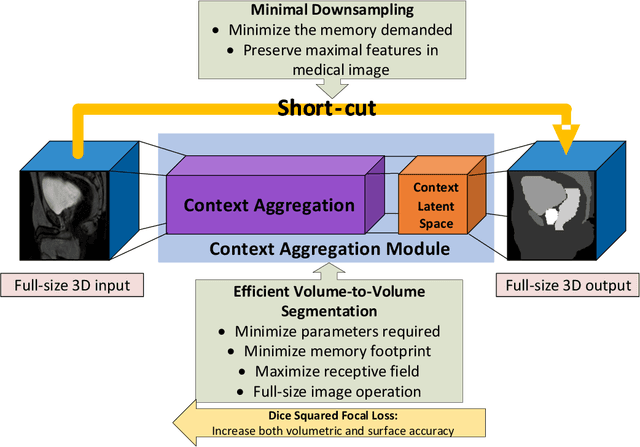
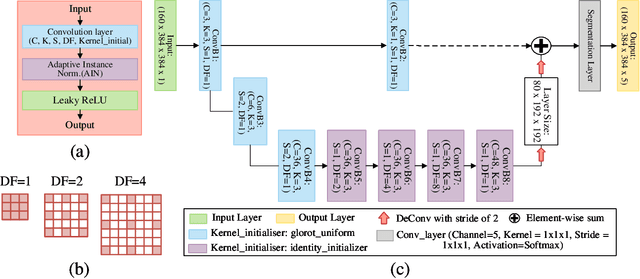
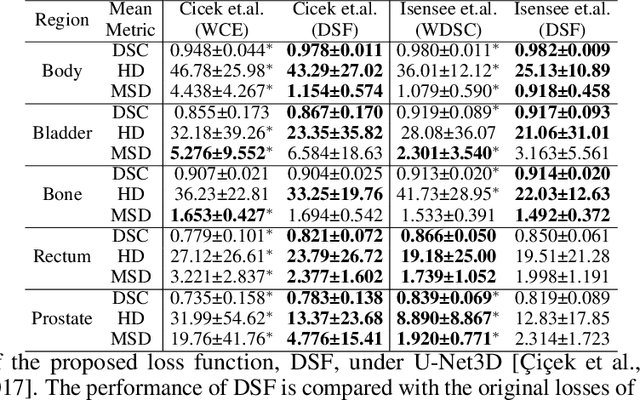
Direct automatic segmentation of objects from 3D medical imaging, such as magnetic resonance (MR) imaging, is challenging as it often involves accurately identifying a number of individual objects with complex geometries within a large volume under investigation. To address these challenges, most deep learning approaches typically enhance their learning capability by substantially increasing the complexity or the number of trainable parameters within their models. Consequently, these models generally require long inference time on standard workstations operating clinical MR systems and are restricted to high-performance computing hardware due to their large memory requirement. Further, to fit 3D dataset through these large models using limited computer memory, trade-off techniques such as patch-wise training are often used which sacrifice the fine-scale geometric information from input images which could be clinically significant for diagnostic purposes. To address these challenges, we present a compact convolutional neural network with a shallow memory footprint to efficiently reduce the number of model parameters required for state-of-art performance. This is critical for practical employment as most clinical environments only have low-end hardware with limited computing power and memory. The proposed network can maintain data integrity by directly processing large full-size 3D input volumes with no patches required and significantly reduces the computational time required for both training and inference. We also propose a novel loss function with extra shape constraint to improve the accuracy for imbalanced classes in 3D MR images.