Decomposing stimulus-specific sensory neural information via diffusion models

To understand sensory coding, we must ask not only how much information neurons encode, but also what that information is about. This requires decomposing mutual information into contributions from individual stimuli and stimulus features fundamentally ill-posed problem with infinitely many possible solutions. We address this by introducing three core axioms, additivity, positivity, and locality that any meaningful stimulus-wise decomposition should satisfy. We then derive a decomposition that meets all three criteria and remains tractable for high-dimensional stimuli. Our decomposition can be efficiently estimated using diffusion models, allowing for scaling up to complex, structured and naturalistic stimuli. Applied to a model of visual neurons, our method quantifies how specific stimuli and features contribute to encoded information. Our approach provides a scalable, interpretable tool for probing representations in both biological and artificial neural systems.

Human-in-the-Loop Optimization for Deep Stimulus Encoding in Visual Prostheses

Neuroprostheses show potential in restoring lost sensory function and enhancing human capabilities, but the sensations produced by current devices often seem unnatural or distorted. Exact placement of implants and differences in individual perception lead to significant variations in stimulus response, making personalized stimulus optimization a key challenge. Bayesian optimization could be used to optimize patient-specific stimulation parameters with limited noisy observations, but is not feasible for high-dimensional stimuli. Alternatively, deep learning models can optimize stimulus encoding strategies, but typically assume perfect knowledge of patient-specific variations. Here we propose a novel, practically feasible approach that overcomes both of these fundamental limitations. First, a deep encoder network is trained to produce optimal stimuli for any individual patient by inverting a forward model mapping electrical stimuli to visual percepts. Second, a preferential Bayesian optimization strategy utilizes this encoder to optimize patient-specific parameters for a new patient, using a minimal number of pairwise comparisons between candidate stimuli. We demonstrate the viability of this approach on a novel, state-of-the-art visual prosthesis model. We show that our approach quickly learns a personalized stimulus encoder, leads to dramatic improvements in the quality of restored vision, and is robust to noisy patient feedback and misspecifications in the underlying forward model. Overall, our results suggest that combining the strengths of deep learning and Bayesian optimization could significantly improve the perceptual experience of patients fitted with visual prostheses and may prove a viable solution for a range of neuroprosthetic technologies.

Contextual Bayesian optimization with binary outputs

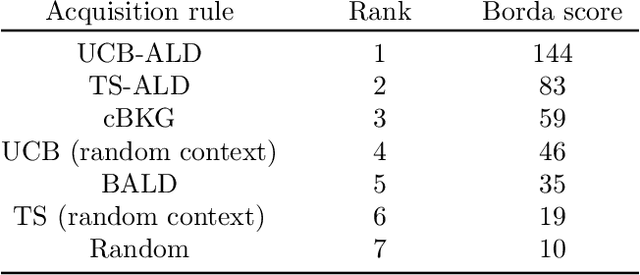
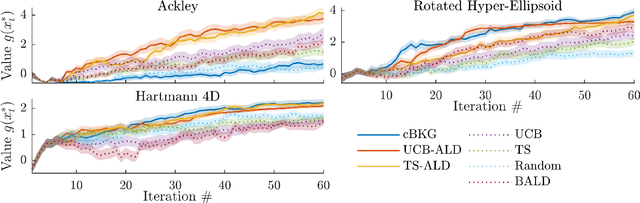
Bayesian optimization (BO) is an efficient method to optimize expensive black-box functions. It has been generalized to scenarios where objective function evaluations return stochastic binary feedback, such as success/failure in a given test, or preference between different parameter settings. In many real-world situations, the objective function can be evaluated in controlled 'contexts' or 'environments' that directly influence the observations. For example, one could directly alter the 'difficulty' of the test that is used to evaluate a system's performance. With binary feedback, the context determines the information obtained from each observation. For example, if the test is too easy/hard, the system will always succeed/fail, yielding uninformative binary outputs. Here we combine ideas from Bayesian active learning and optimization to efficiently choose the best context and optimization parameter on each iteration. We demonstrate the performance of our algorithm and illustrate how it can be used to tackle a concrete application in visual psychophysics: efficiently improving patients' vision via corrective lenses, using psychophysics measurements.

Efficient Exploration in Binary and Preferential Bayesian Optimization

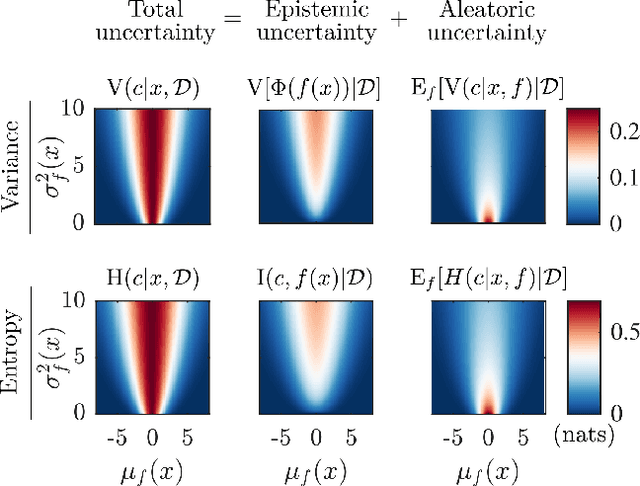
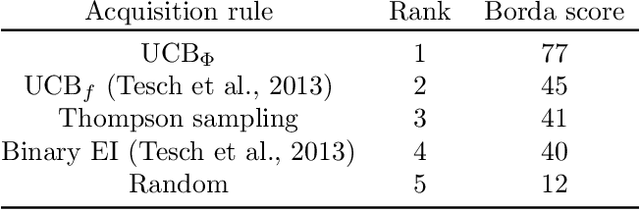
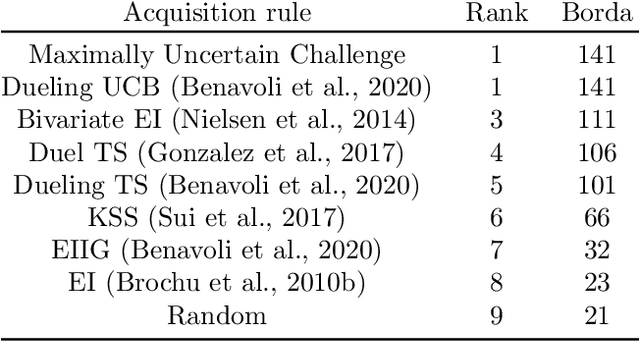
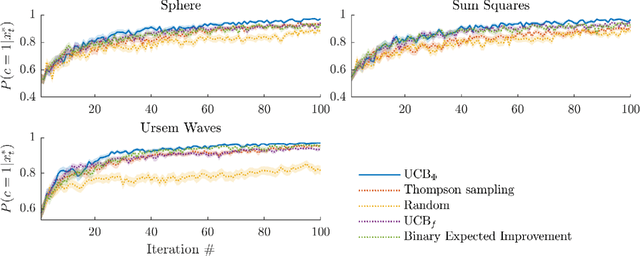
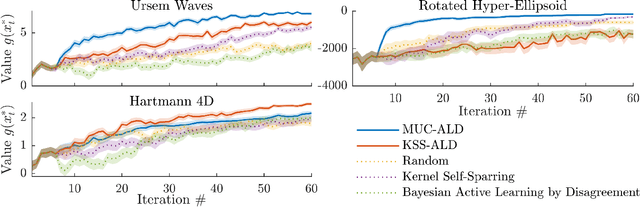
Bayesian optimization (BO) is an effective approach to optimize expensive black-box functions, that seeks to trade-off between exploitation (selecting parameters where the maximum is likely) and exploration (selecting parameters where we are uncertain about the objective function). In many real-world situations, direct measurements of the objective function are not possible, and only binary measurements such as success/failure or pairwise comparisons are available. To perform efficient exploration in this setting, we show that it is important for BO algorithms to distinguish between different types of uncertainty: epistemic uncertainty, about the unknown objective function, and aleatoric uncertainty, which comes from noisy observations and cannot be reduced. In effect, only the former is important for efficient exploration. Based on this, we propose several new acquisition functions that outperform state-of-the-art heuristics in binary and preferential BO, while being fast to compute and easy to implement. We then generalize these acquisition rules to batch learning, where multiple queries are performed simultaneously.

Relevant sparse codes with variational information bottleneck

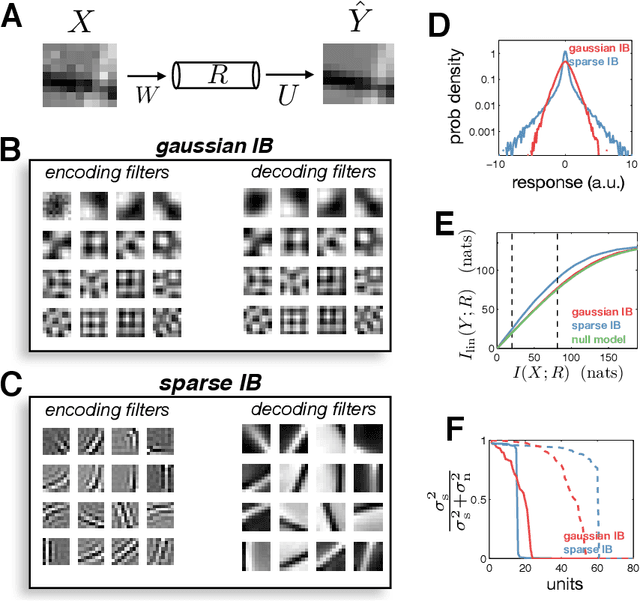
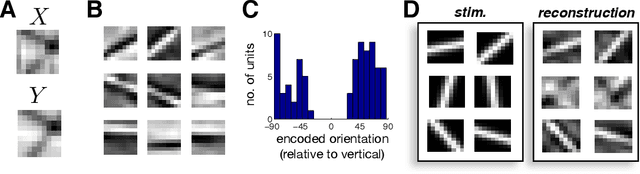
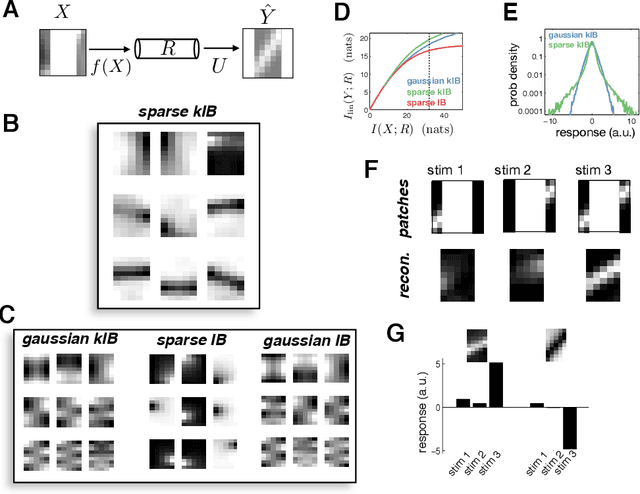
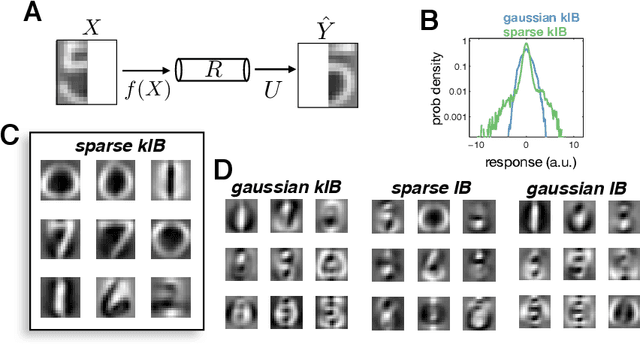
In many applications, it is desirable to extract only the relevant aspects of data. A principled way to do this is the information bottleneck (IB) method, where one seeks a code that maximizes information about a 'relevance' variable, Y, while constraining the information encoded about the original data, X. Unfortunately however, the IB method is computationally demanding when data are high-dimensional and/or non-gaussian. Here we propose an approximate variational scheme for maximizing a lower bound on the IB objective, analogous to variational EM. Using this method, we derive an IB algorithm to recover features that are both relevant and sparse. Finally, we demonstrate how kernelized versions of the algorithm can be used to address a broad range of problems with non-linear relation between X and Y.