Relevant sparse codes with variational information bottleneck
Paper and Code
Oct 26, 2016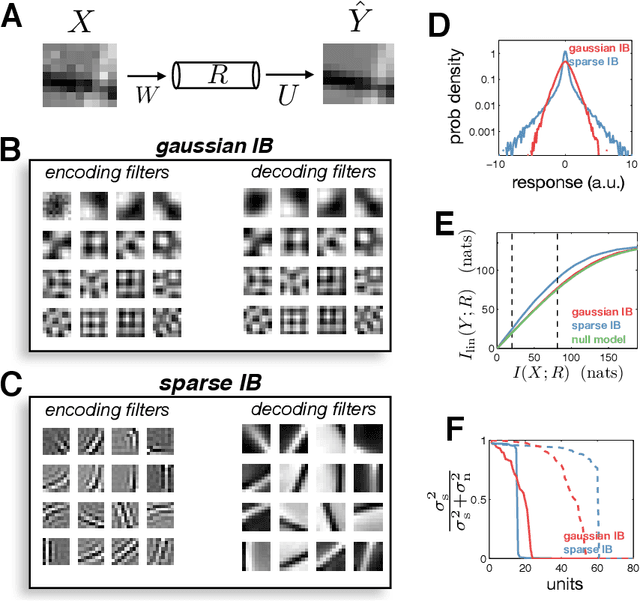
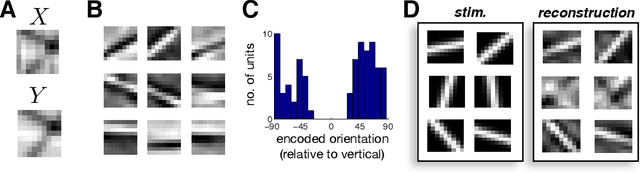
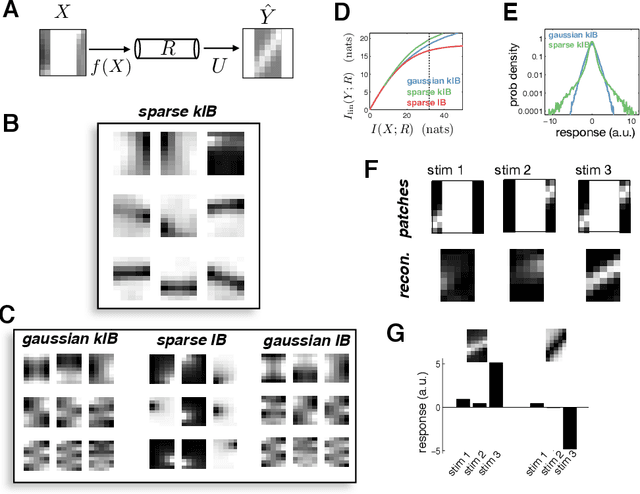
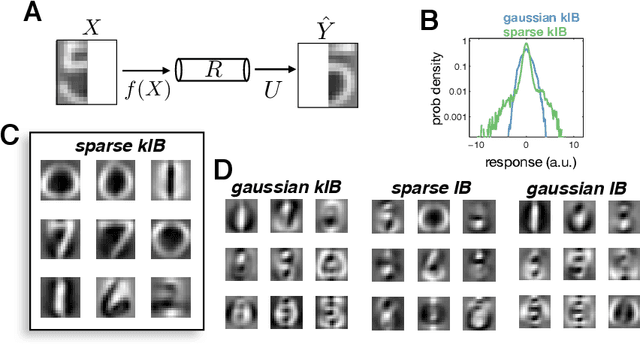
In many applications, it is desirable to extract only the relevant aspects of data. A principled way to do this is the information bottleneck (IB) method, where one seeks a code that maximizes information about a 'relevance' variable, Y, while constraining the information encoded about the original data, X. Unfortunately however, the IB method is computationally demanding when data are high-dimensional and/or non-gaussian. Here we propose an approximate variational scheme for maximizing a lower bound on the IB objective, analogous to variational EM. Using this method, we derive an IB algorithm to recover features that are both relevant and sparse. Finally, we demonstrate how kernelized versions of the algorithm can be used to address a broad range of problems with non-linear relation between X and Y.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge