Convolution goes higher-order: a biologically inspired mechanism empowers image classification

We propose a novel approach to image classification inspired by complex nonlinear biological visual processing, whereby classical convolutional neural networks (CNNs) are equipped with learnable higher-order convolutions. Our model incorporates a Volterra-like expansion of the convolution operator, capturing multiplicative interactions akin to those observed in early and advanced stages of biological visual processing. We evaluated this approach on synthetic datasets by measuring sensitivity to testing higher-order correlations and performance in standard benchmarks (MNIST, FashionMNIST, CIFAR10, CIFAR100 and Imagenette). Our architecture outperforms traditional CNN baselines, and achieves optimal performance with expansions up to 3rd/4th order, aligning remarkably well with the distribution of pixel intensities in natural images. Through systematic perturbation analysis, we validate this alignment by isolating the contributions of specific image statistics to model performance, demonstrating how different orders of convolution process distinct aspects of visual information. Furthermore, Representational Similarity Analysis reveals distinct geometries across network layers, indicating qualitatively different modes of visual information processing. Our work bridges neuroscience and deep learning, offering a path towards more effective, biologically inspired computer vision models. It provides insights into visual information processing and lays the groundwork for neural networks that better capture complex visual patterns, particularly in resource-constrained scenarios.

A new inference approach for training shallow and deep generalized linear models of noisy interacting neurons

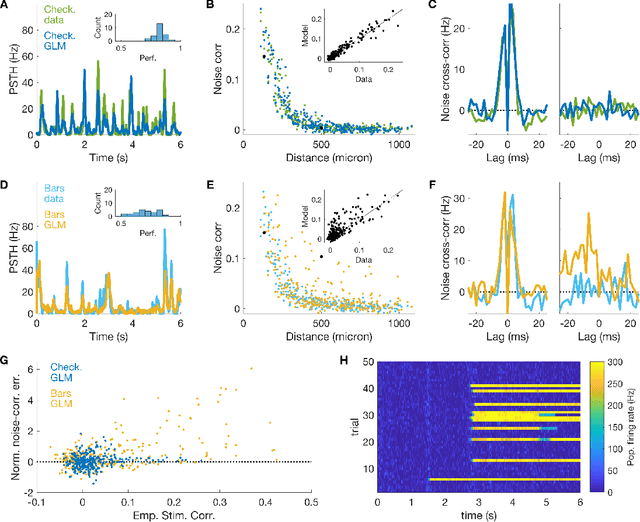
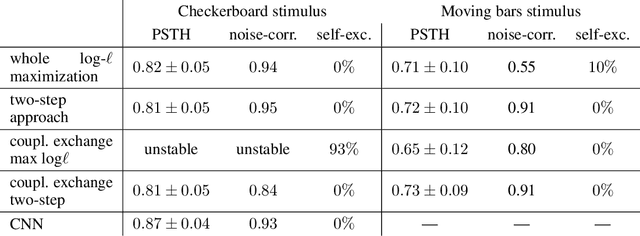
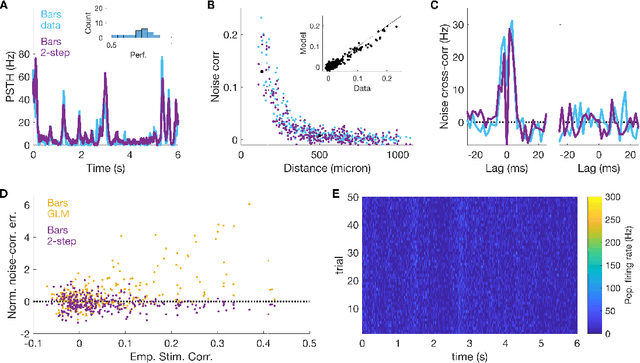
Generalized linear models are one of the most efficient paradigms for predicting the correlated stochastic activity of neuronal networks in response to external stimuli, with applications in many brain areas. However, when dealing with complex stimuli, their parameters often do not generalize across different stimulus statistics, leading to degraded performance and blowup instabilities. Here, we develop a two-step inference strategy that allows us to train robust generalized linear models of interacting neurons, by explicitly separating the effects of stimulus correlations and noise correlations in each training step. Applying this approach to the responses of retinal ganglion cells to complex visual stimuli, we show that, compared to classical methods, the models trained in this way exhibit improved performance, are more stable, yield robust interaction networks, and generalize well across complex visual statistics. The method can be extended to deep convolutional neural networks, leading to models with high predictive accuracy for both the neuron firing rates and their correlations.

Relevant sparse codes with variational information bottleneck

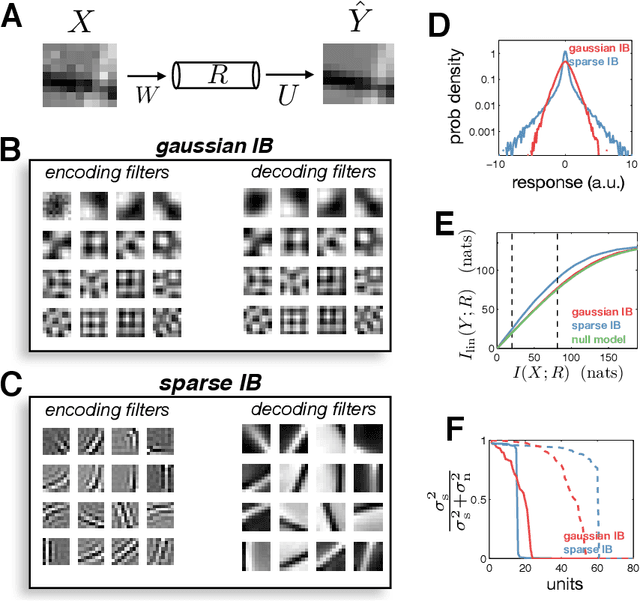
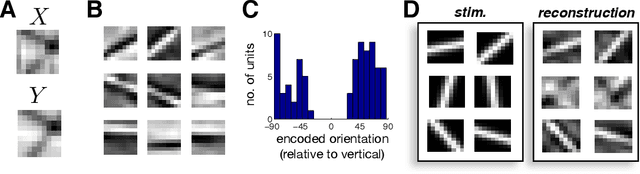
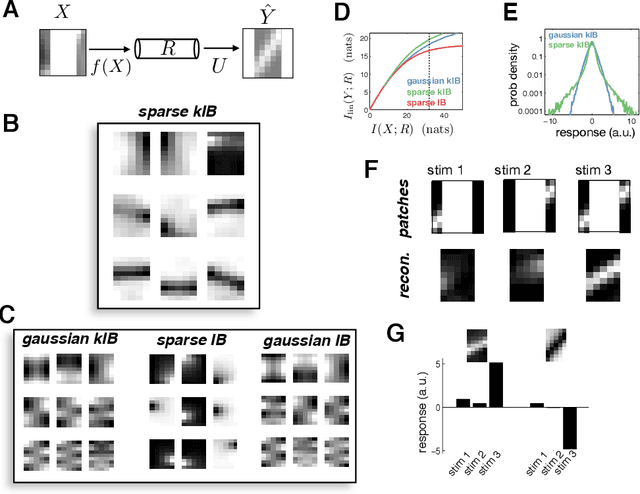
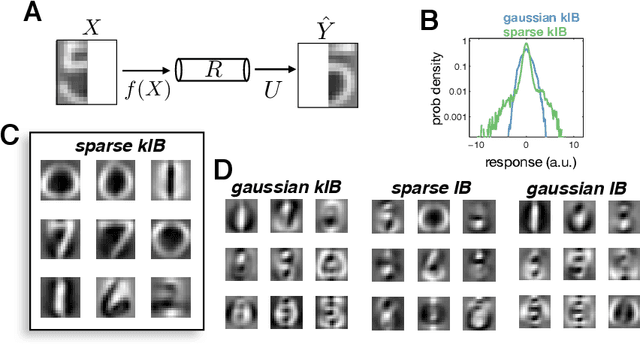
In many applications, it is desirable to extract only the relevant aspects of data. A principled way to do this is the information bottleneck (IB) method, where one seeks a code that maximizes information about a 'relevance' variable, Y, while constraining the information encoded about the original data, X. Unfortunately however, the IB method is computationally demanding when data are high-dimensional and/or non-gaussian. Here we propose an approximate variational scheme for maximizing a lower bound on the IB objective, analogous to variational EM. Using this method, we derive an IB algorithm to recover features that are both relevant and sparse. Finally, we demonstrate how kernelized versions of the algorithm can be used to address a broad range of problems with non-linear relation between X and Y.