Contextual Bayesian optimization with binary outputs
Paper and Code
Nov 05, 2021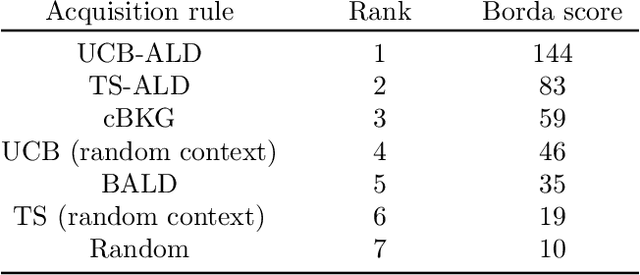
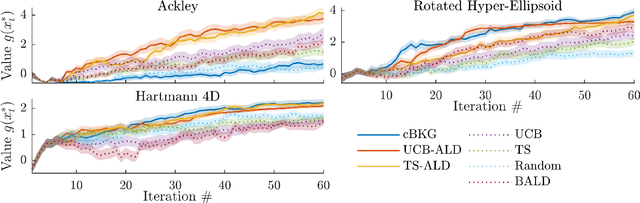

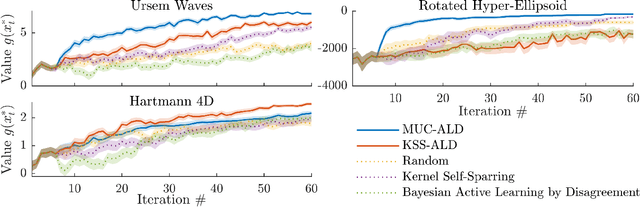
Bayesian optimization (BO) is an efficient method to optimize expensive black-box functions. It has been generalized to scenarios where objective function evaluations return stochastic binary feedback, such as success/failure in a given test, or preference between different parameter settings. In many real-world situations, the objective function can be evaluated in controlled 'contexts' or 'environments' that directly influence the observations. For example, one could directly alter the 'difficulty' of the test that is used to evaluate a system's performance. With binary feedback, the context determines the information obtained from each observation. For example, if the test is too easy/hard, the system will always succeed/fail, yielding uninformative binary outputs. Here we combine ideas from Bayesian active learning and optimization to efficiently choose the best context and optimization parameter on each iteration. We demonstrate the performance of our algorithm and illustrate how it can be used to tackle a concrete application in visual psychophysics: efficiently improving patients' vision via corrective lenses, using psychophysics measurements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge