Using Spatial Diffusions for Optoacoustic Tomography Image Reconstruction

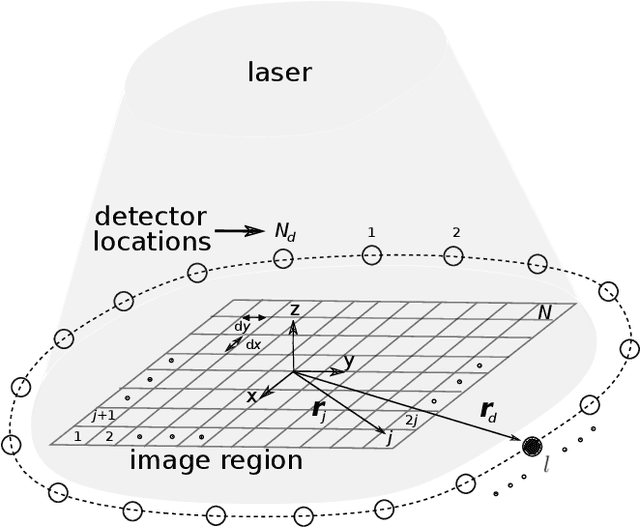
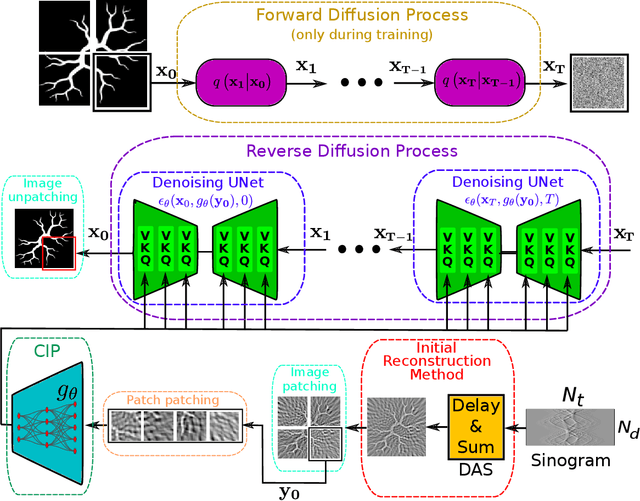
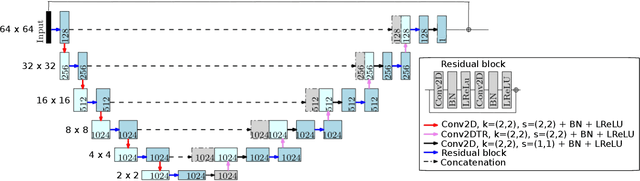
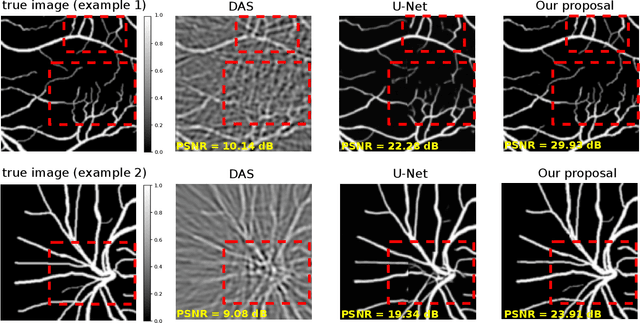
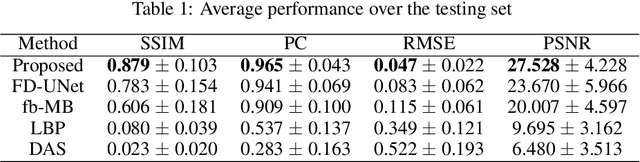
Optoacoustic tomography image reconstruction has been a problem of interest in recent years. By exploiting the exceptional generative power of the recently proposed diffusion models we consider a scheme which is based on a conditional diffusion process. Using a simple initial image reconstruction method such as Delay and Sum, we consider a specially designed autoencoder architecture which generates a latent representation which is used as conditional information in the generative diffusion process. Numerical results show the merits of our proposal in terms of quality metrics such as PSNR and SSIM, showing that the conditional information generated in terms of the initial reconstructed image is able to bias the generative process of the diffusion model in order to enhance the image, correct artifacts and even recover some finer details that the initial reconstruction method is not able to obtain.

On the Convergence of Semi Unsupervised Calibration through Prior Adaptation Algorithm

Calibration is an essential key in machine leaning. Semi Unsupervised Calibration through Prior Adaptation (SUCPA) is a calibration algorithm used in (but not limited to) large-scale language models defined by a {system of first-order difference equation. The map derived by this system} has the peculiarity of being non-hyperbolic {with a non-bounded set of non-isolated fixed points}. In this work, we prove several convergence properties of this algorithm from the perspective of dynamical systems. For a binary classification problem, it can be shown that the algorithm always converges, {more precisely, the map is globally asymptotically stable, and the orbits converge} to a single line of fixed points. Finally, we perform numerical experiments on real-world application to support the presented results. Experiment codes are available online.

Invariant Representations in Deep Learning for Optoacoustic Imaging

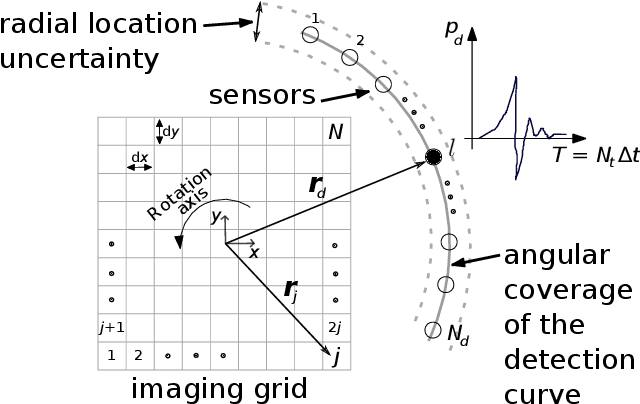
Image reconstruction in optoacoustic tomography (OAT) is a trending learning task highly dependent on measured physical magnitudes present at sensing time. The large number of different settings, and also the presence of uncertainties or partial knowledge of parameters, can lead to reconstructions algorithms that are specifically tailored and designed to a particular configuration which could not be the one that will be ultimately faced in a final practical situation. Being able to learn reconstruction algorithms that are robust to different environments (e.g. the different OAT image reconstruction settings) or invariant to such environments is highly valuable because it allows to focus on what truly matters for the application at hand and discard what are considered spurious features. In this work we explore the use of deep learning algorithms based on learning invariant and robust representations for the OAT inverse problem. In particular, we consider the application of the ANDMask scheme due to its easy adaptation to the OAT problem. Numerical experiments are conducted showing that, when out-of-distribution generalization (against variations in parameters such as the location of the sensors) is imposed, there is no degradation of the performance and, in some cases, it is even possible to achieve improvements with respect to standard deep learning approaches where invariance robustness is not explicitly considered.

Cross-domain Sentiment Classification in Spanish

Sentiment Classification is a fundamental task in the field of Natural Language Processing, and has very important academic and commercial applications. It aims to automatically predict the degree of sentiment present in a text that contains opinions and subjectivity at some level, like product and movie reviews, or tweets. This can be really difficult to accomplish, in part, because different domains of text contains different words and expressions. In addition, this difficulty increases when text is written in a non-English language due to the lack of databases and resources. As a consequence, several cross-domain and cross-language techniques are often applied to this task in order to improve the results. In this work we perform a study on the ability of a classification system trained with a large database of product reviews to generalize to different Spanish domains. Reviews were collected from the MercadoLibre website from seven Latin American countries, allowing the creation of a large and balanced dataset. Results suggest that generalization across domains is feasible though very challenging when trained with these product reviews, and can be improved by pre-training and fine-tuning the classification model.

Combining band-frequency separation and deep neural networks for optoacoustic imaging

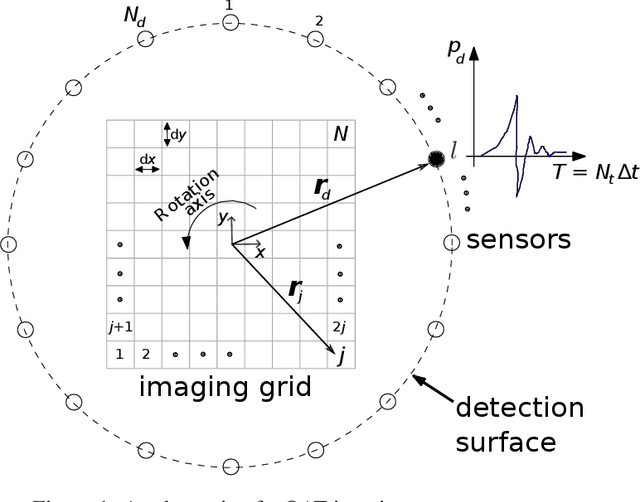
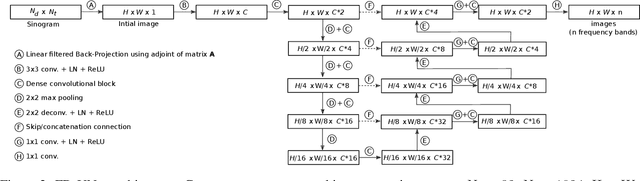
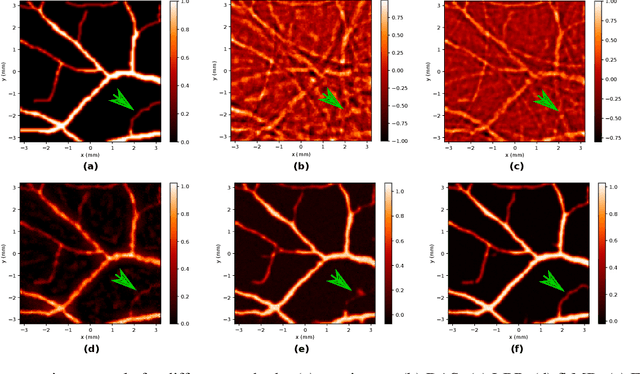
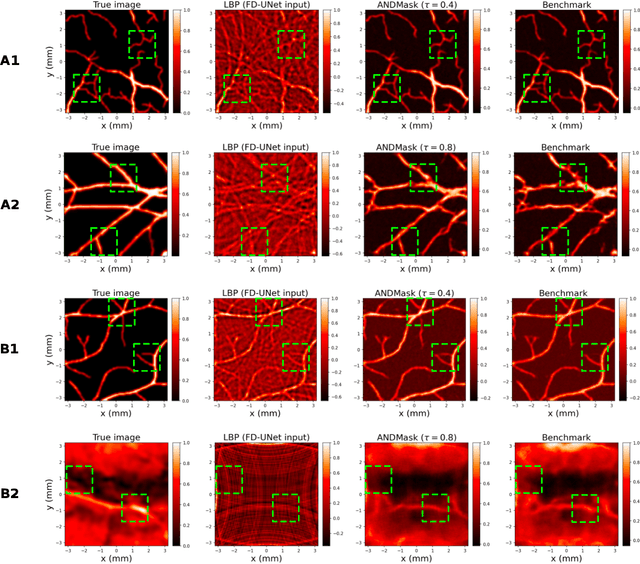
In this paper we consider the problem of image reconstruction in optoacoustic tomography. In particular, we devise a deep neural architecture that can explicitly take into account the band-frequency information contained in the sinogram. This is accomplished by two means. First, we jointly use a linear filtered back-projection method and a fully dense UNet for the generation of the images corresponding to each one of the frequency bands considered in the separation. Secondly, in order to train the model, we introduce a special loss function consisting of three terms: (i) a separating frequency bands term; (ii) a sinogram-based consistency term and (iii) a term that directly measures the quality of image reconstruction and which takes advantage of the presence of ground-truth images present in training dataset. Numerical experiments show that the proposed model, which can be easily trainable by standard optimization methods, presents an excellent generalization performance quantified by a number of metrics commonly used in practice. Also, in the testing phase, our solution has a comparable (in some cases lower) computational complexity, which is a desirable feature for real-time implementation of optoacoustic imaging.

PACMAN: PAC-style bounds accounting for the Mismatch between Accuracy and Negative log-loss

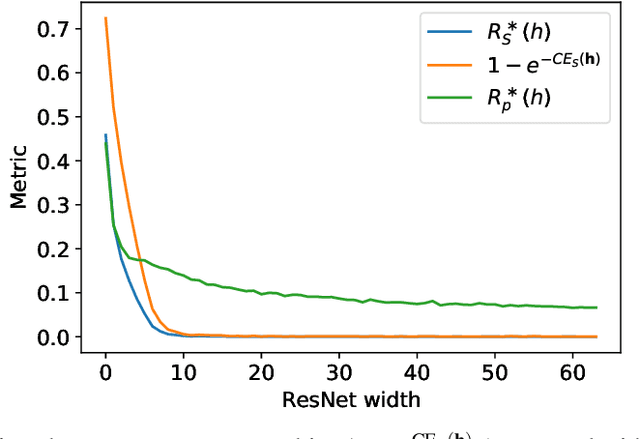
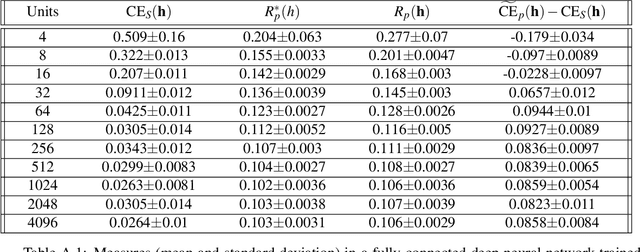
The ultimate performance of machine learning algorithms for classification tasks is usually measured in terms of the empirical error probability (or accuracy) based on a testing dataset. Whereas, these algorithms are optimized through the minimization of a typically different--more convenient--loss function based on a training set. For classification tasks, this loss function is often the negative log-loss that leads to the well-known cross-entropy risk which is typically better behaved (from a numerical perspective) than the error probability. Conventional studies on the generalization error do not usually take into account the underlying mismatch between losses at training and testing phases. In this work, we introduce an analysis based on point-wise PAC approach over the generalization gap considering the mismatch of testing based on the accuracy metric and training on the negative log-loss. We label this analysis PACMAN. Building on the fact that the mentioned mismatch can be written as a likelihood ratio, concentration inequalities can be used to provide some insights for the generalization problem in terms of some point-wise PAC bounds depending on some meaningful information-theoretic quantities. An analysis of the obtained bounds and a comparison with available results in the literature are also provided.

The Role of Mutual Information in Variational Classifiers

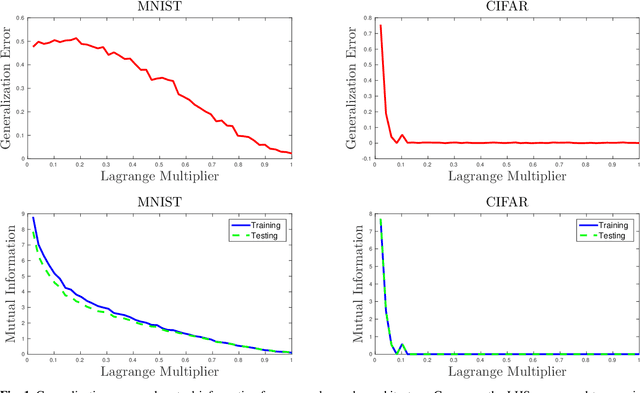
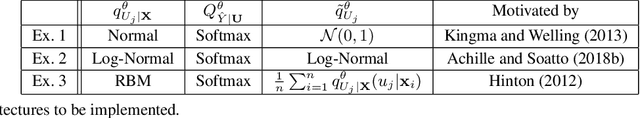
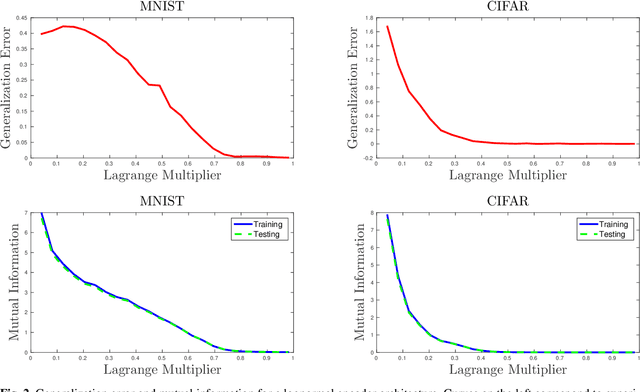
Overfitting data is a well-known phenomenon related with the generation of a model that mimics too closely (or exactly) a particular instance of data, and may therefore fail to predict future observations reliably. In practice, this behaviour is controlled by various--sometimes heuristics--regularization techniques, which are motivated by developing upper bounds to the generalization error. In this work, we study the generalization error of classifiers relying on stochastic encodings trained on the cross-entropy loss, which is often used in deep learning for classification problems. We derive bounds to the generalization error showing that there exists a regime where the generalization error is bounded by the mutual information between input features and the corresponding representations in the latent space, which are randomly generated according to the encoding distribution. Our bounds provide an information-theoretic understanding of generalization in the so-called class of variational classifiers, which are regularized by a Kullback-Leibler (KL) divergence term. These results give theoretical grounds for the highly popular KL term in variational inference methods that was already recognized to act effectively as a regularization penalty. We further observe connections with well studied notions such as Variational Autoencoders, Information Dropout, Information Bottleneck and Boltzmann Machines. Finally, we perform numerical experiments on MNIST and CIFAR datasets and show that mutual information is indeed highly representative of the behaviour of the generalization error.

Understanding the Behaviour of the Empirical Cross-Entropy Beyond the Training Distribution

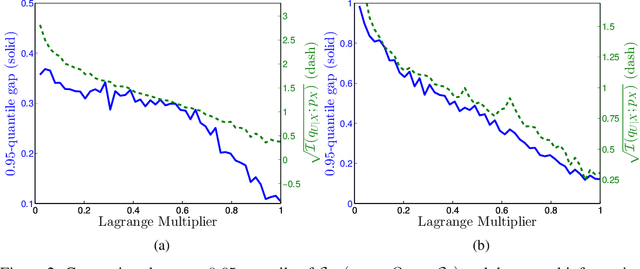
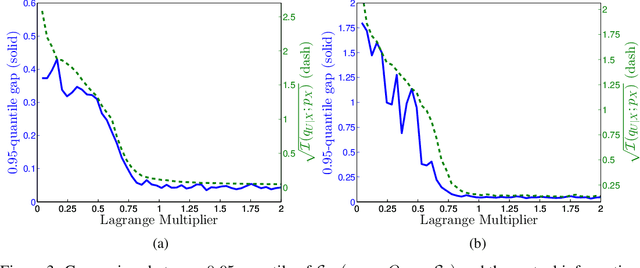
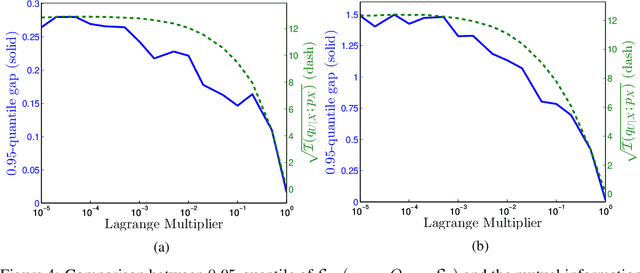
Machine learning theory has mostly focused on generalization to samples from the same distribution as the training data. Whereas a better understanding of generalization beyond the training distribution where the observed distribution changes is also fundamentally important to achieve a more powerful form of generalization. In this paper, we attempt to study through the lens of information measures how a particular architecture behaves when the true probability law of the samples is potentially different at training and testing times. Our main result is that the testing gap between the empirical cross-entropy and its statistical expectation (measured with respect to the testing probability law) can be bounded with high probability by the mutual information between the input testing samples and the corresponding representations, generated by the encoder obtained at training time. These results of theoretical nature are supported by numerical simulations showing that the mentioned mutual information is representative of the testing gap, capturing qualitatively the dynamic in terms of the hyperparameters of the network.