PACMAN: PAC-style bounds accounting for the Mismatch between Accuracy and Negative log-loss
Paper and Code
Dec 10, 2021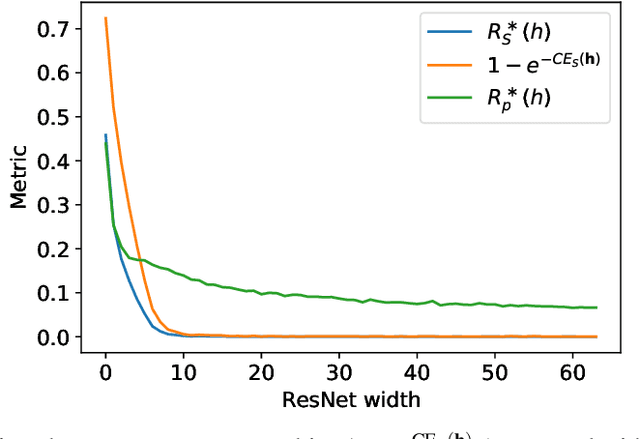
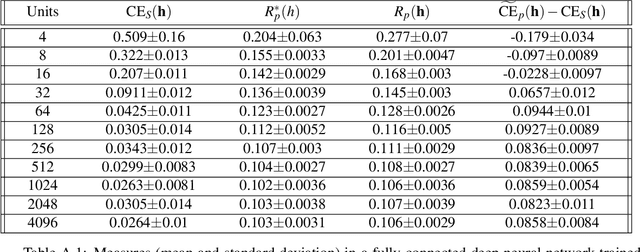
The ultimate performance of machine learning algorithms for classification tasks is usually measured in terms of the empirical error probability (or accuracy) based on a testing dataset. Whereas, these algorithms are optimized through the minimization of a typically different--more convenient--loss function based on a training set. For classification tasks, this loss function is often the negative log-loss that leads to the well-known cross-entropy risk which is typically better behaved (from a numerical perspective) than the error probability. Conventional studies on the generalization error do not usually take into account the underlying mismatch between losses at training and testing phases. In this work, we introduce an analysis based on point-wise PAC approach over the generalization gap considering the mismatch of testing based on the accuracy metric and training on the negative log-loss. We label this analysis PACMAN. Building on the fact that the mentioned mismatch can be written as a likelihood ratio, concentration inequalities can be used to provide some insights for the generalization problem in terms of some point-wise PAC bounds depending on some meaningful information-theoretic quantities. An analysis of the obtained bounds and a comparison with available results in the literature are also provided.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge