Understanding the Behaviour of the Empirical Cross-Entropy Beyond the Training Distribution

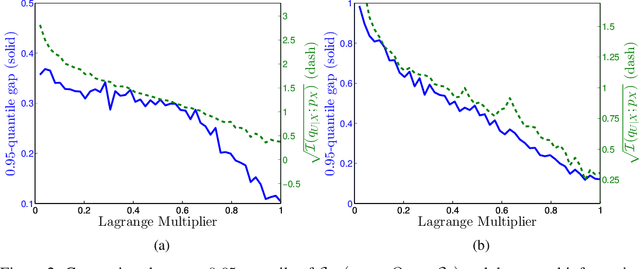
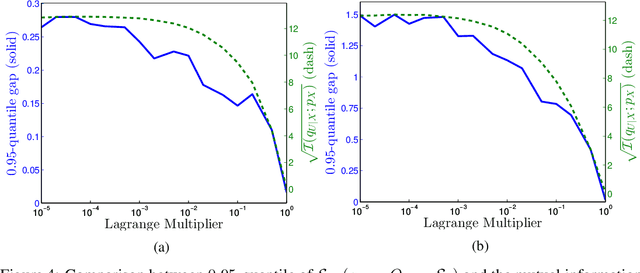
Machine learning theory has mostly focused on generalization to samples from the same distribution as the training data. Whereas a better understanding of generalization beyond the training distribution where the observed distribution changes is also fundamentally important to achieve a more powerful form of generalization. In this paper, we attempt to study through the lens of information measures how a particular architecture behaves when the true probability law of the samples is potentially different at training and testing times. Our main result is that the testing gap between the empirical cross-entropy and its statistical expectation (measured with respect to the testing probability law) can be bounded with high probability by the mutual information between the input testing samples and the corresponding representations, generated by the encoder obtained at training time. These results of theoretical nature are supported by numerical simulations showing that the mentioned mutual information is representative of the testing gap, capturing qualitatively the dynamic in terms of the hyperparameters of the network.