Convergence Analysis of Decentralized ASGD

Over the last decades, Stochastic Gradient Descent (SGD) has been intensively studied by the Machine Learning community. Despite its versatility and excellent performance, the optimization of large models via SGD still is a time-consuming task. To reduce training time, it is common to distribute the training process across multiple devices. Recently, it has been shown that the convergence of asynchronous SGD (ASGD) will always be faster than mini-batch SGD. However, despite these improvements in the theoretical bounds, most ASGD convergence-rate proofs still rely on a centralized parameter server, which is prone to become a bottleneck when scaling out the gradient computations across many distributed processes. In this paper, we present a novel convergence-rate analysis for decentralized and asynchronous SGD (DASGD) which does not require partial synchronization among nodes nor restrictive network topologies. Specifically, we provide a bound of $\mathcal{O}(\sigma\epsilon^{-2}) + \mathcal{O}(QS_{avg}\epsilon^{-3/2}) + \mathcal{O}(S_{avg}\epsilon^{-1})$ for the convergence rate of DASGD, where $S_{avg}$ is the average staleness between models, $Q$ is a constant that bounds the norm of the gradients, and $\epsilon$ is a (small) error that is allowed within the bound. Furthermore, when gradients are not bounded, we prove the convergence rate of DASGD to be $\mathcal{O}(\sigma\epsilon^{-2}) + \mathcal{O}(\sqrt{\hat{S}_{avg}\hat{S}_{max}}\epsilon^{-1})$, with $\hat{S}_{max}$ and $\hat{S}_{avg}$ representing a loose version of the average and maximum staleness, respectively. Our convergence proof holds for a fixed stepsize and any non-convex, homogeneous, and L-smooth objective function. We anticipate that our results will be of high relevance for the adoption of DASGD by a broad community of researchers and developers.

OPTWIN: Drift identification with optimal sub-windows

Online Learning (OL) is a field of research that is increasingly gaining attention both in academia and industry. One of the main challenges of OL is the inherent presence of concept drifts, which are commonly defined as unforeseeable changes in the statistical properties of an incoming data stream over time. The detection of concept drifts typically involves analyzing the error rates produced by an underlying OL algorithm in order to identify if a concept drift occurred or not, such that the OL algorithm can adapt accordingly. Current concept-drift detectors perform very well, i.e., with low false negative rates, but they still tend to exhibit high false positive rates in the concept-drift detection. This may impact the performance of the learner and result in an undue amount of computational resources spent on retraining a model that actually still performs within its expected range. In this paper, we propose OPTWIN, our "OPTimal WINdow" concept drift detector. OPTWIN uses a sliding window of events over an incoming data stream to track the errors of an OL algorithm. The novelty of OPTWIN is to consider both the means and the variances of the error rates produced by a learner in order to split the sliding window into two provably optimal sub-windows, such that the split occurs at the earliest event at which a statistically significant difference according to either the $t$- or the $f$-tests occurred. We assessed OPTWIN over the MOA framework, using ADWIN, DDM, EDDM, STEPD and ECDD as baselines over 7 synthetic and real-world datasets, and in the presence of both sudden and gradual concept drifts. In our experiments, we show that OPTWIN surpasses the F1-score of the baselines in a statistically significant manner while maintaining a lower detection delay and saving up to 21% of time spent on retraining the models.

Enriching Relation Extraction with OpenIE

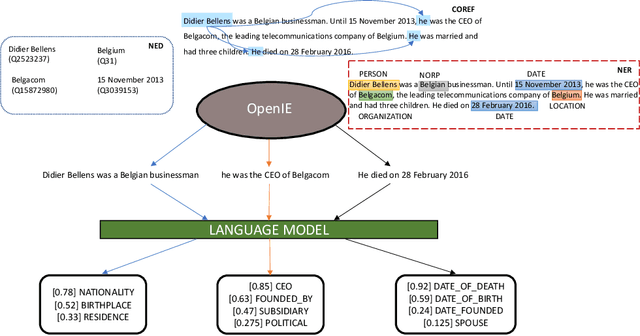
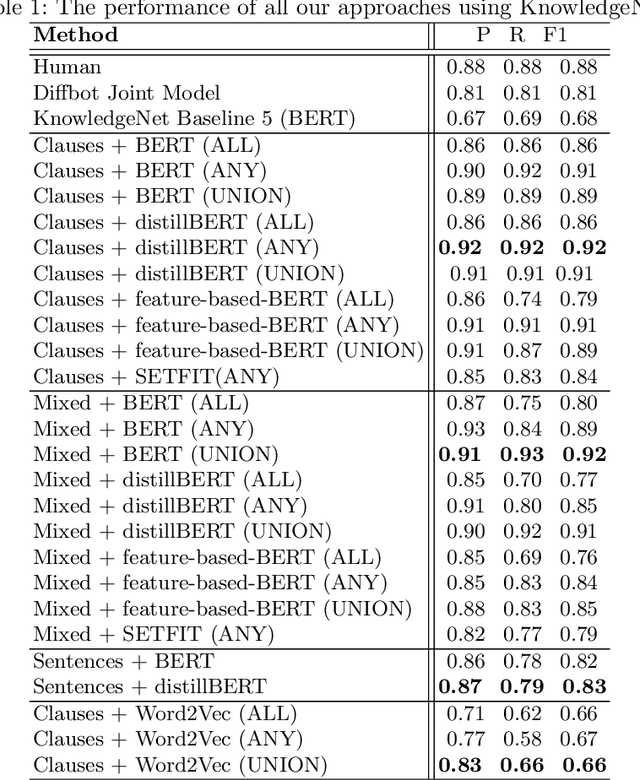
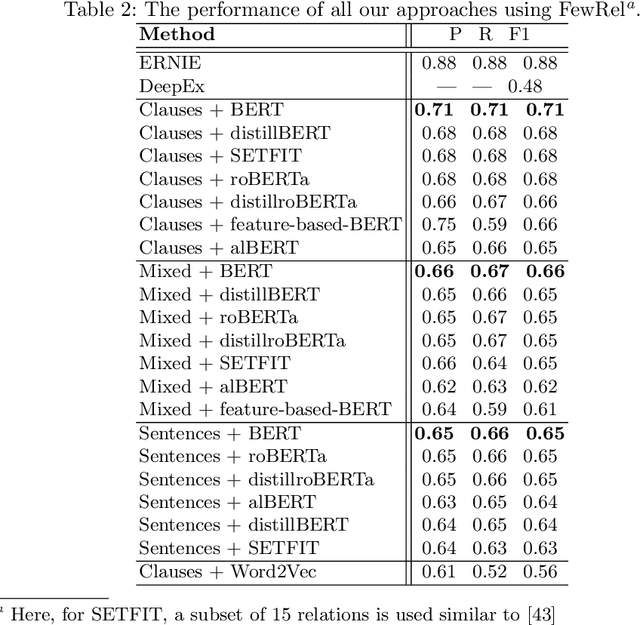
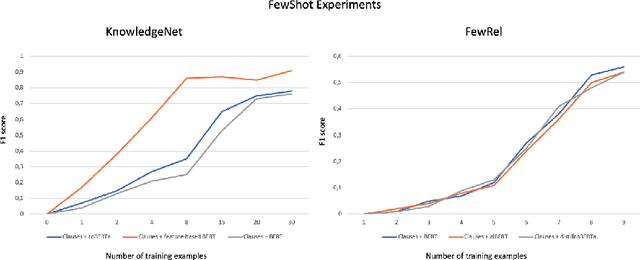
Relation extraction (RE) is a sub-discipline of information extraction (IE) which focuses on the prediction of a relational predicate from a natural-language input unit (such as a sentence, a clause, or even a short paragraph consisting of multiple sentences and/or clauses). Together with named-entity recognition (NER) and disambiguation (NED), RE forms the basis for many advanced IE tasks such as knowledge-base (KB) population and verification. In this work, we explore how recent approaches for open information extraction (OpenIE) may help to improve the task of RE by encoding structured information about the sentences' principal units, such as subjects, objects, verbal phrases, and adverbials, into various forms of vectorized (and hence unstructured) representations of the sentences. Our main conjecture is that the decomposition of long and possibly convoluted sentences into multiple smaller clauses via OpenIE even helps to fine-tune context-sensitive language models such as BERT (and its plethora of variants) for RE. Our experiments over two annotated corpora, KnowledgeNet and FewRel, demonstrate the improved accuracy of our enriched models compared to existing RE approaches. Our best results reach 92% and 71% of F1 score for KnowledgeNet and FewRel, respectively, proving the effectiveness of our approach on competitive benchmarks.

BigText-QA: Question Answering over a Large-Scale Hybrid Knowledge Graph

Answering complex questions over textual resources remains a challenging problem$\unicode{x2013}$especially when interpreting the fine-grained relationships among multiple entities that occur within a natural-language question or clue. Curated knowledge bases (KBs), such as YAGO, DBpedia, Freebase and Wikidata, have been widely used in this context and gained great acceptance for question-answering (QA) applications in the past decade. While current KBs offer a concise representation of structured knowledge, they lack the variety of formulations and semantic nuances as well as the context of information provided by the natural-language sources. With BigText-QA, we aim to develop an integrated QA system which is able to answer questions based on a more redundant form of a knowledge graph (KG) that organizes both structured and unstructured (i.e., "hybrid") knowledge in a unified graphical representation. BigText-QA thereby is able to combine the best of both worlds$\unicode{x2013}$a canonical set of named entities, mapped to a structured background KB (such as YAGO or Wikidata), as well as an open set of textual clauses providing highly diversified relational paraphrases with rich context information.

TensAIR: Online Learning from Data Streams via Asynchronous Iterative Routing

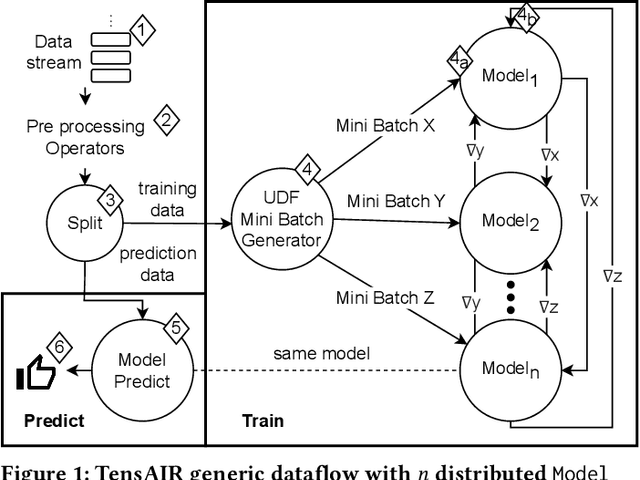
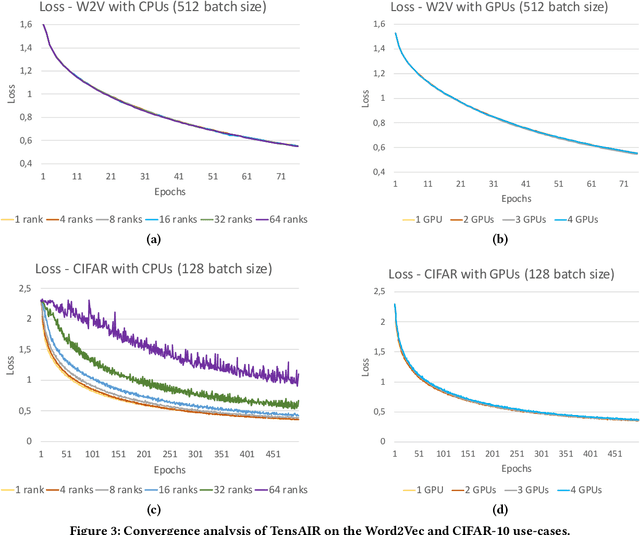
Online learning (OL) from data streams is an emerging area of research that encompasses numerous challenges from stream processing, machine learning, and networking. Recent extensions of stream-processing platforms, such as Apache Kafka and Flink, already provide basic extensions for the training of neural networks in a stream-processing pipeline. However, these extensions are not scalable and flexible enough for many real-world use-cases, since they do not integrate the neural-network libraries as a first-class citizen into their architectures. In this paper, we present TensAIR, which provides an end-to-end dataflow engine for OL from data streams via a protocol to which we refer as asynchronous iterative routing. TensAIR supports the common dataflow operators, such as Map, Reduce, Join, and has been augmented by the data-parallel OL functions train and predict. These belong to the new Model operator, in which an initial TensorFlow model (either freshly initialized or pre-trained) is replicated among multiple decentralized worker nodes. Our decentralized architecture allows TensAIR to efficiently shard incoming data batches across the distributed model replicas, which in turn trigger the model updates via asynchronous stochastic gradient descent. We empirically demonstrate that TensAIR achieves a nearly linear scale-out in terms of (1) the number of worker nodes deployed in the network, and (2) the throughput at which the data batches arrive at the dataflow operators. We exemplify the versatility of TensAIR by investigating both sparse (Word2Vec) and dense (CIFAR-10) use-cases, for which we are able to demonstrate very significant performance improvements in comparison to Kafka, Flink, and Horovod. We also demonstrate the magnitude of these improvements by depicting the possibility of real-time concept drift adaptation of a sentiment analysis model trained over a Twitter stream.

Robust and Provable Guarantees for Sparse Random Embeddings

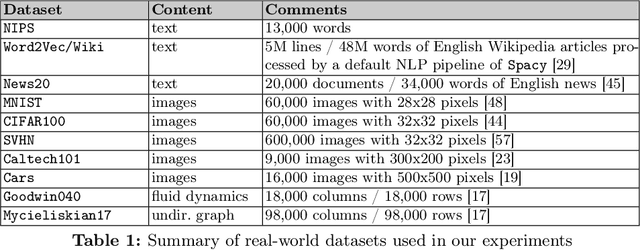
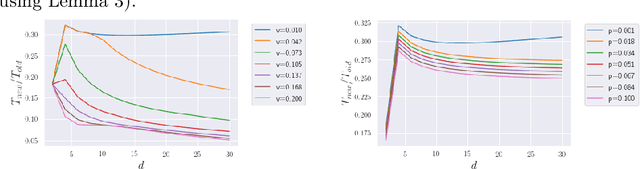
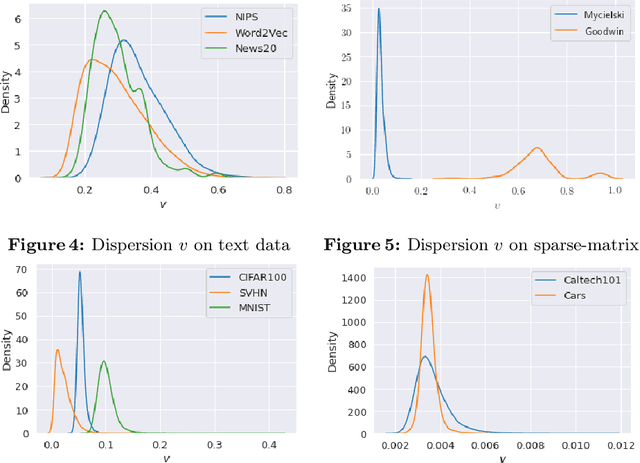
In this work, we improve upon the guarantees for sparse random embeddings, as they were recently provided and analyzed by Freksen at al. (NIPS'18) and Jagadeesan (NIPS'19). Specifically, we show that (a) our bounds are explicit as opposed to the asymptotic guarantees provided previously, and (b) our bounds are guaranteed to be sharper by practically significant constants across a wide range of parameters, including the dimensionality, sparsity and dispersion of the data. Moreover, we empirically demonstrate that our bounds significantly outperform prior works on a wide range of real-world datasets, such as collections of images, text documents represented as bags-of-words, and text sequences vectorized by neural embeddings. Behind our numerical improvements are techniques of broader interest, which improve upon key steps of previous analyses in terms of (c) tighter estimates for certain types of quadratic chaos, (d) establishing extreme properties of sparse linear forms, and (e) improvements on bounds for the estimation of sums of independent random variables.