Exact Non-Oblivious Performance of Rademacher Random Embeddings

This paper revisits the performance of Rademacher random projections, establishing novel statistical guarantees that are numerically sharp and non-oblivious with respect to the input data. More specifically, the central result is the Schur-concavity property of Rademacher random projections with respect to the inputs. This offers a novel geometric perspective on the performance of random projections, while improving quantitatively on bounds from previous works. As a corollary of this broader result, we obtained the improved performance on data which is sparse or is distributed with small spread. This non-oblivious analysis is a novelty compared to techniques from previous work, and bridges the frequently observed gap between theory and practise. The main result uses an algebraic framework for proving Schur-concavity properties, which is a contribution of independent interest and an elegant alternative to derivative-based criteria.

Enriching Relation Extraction with OpenIE

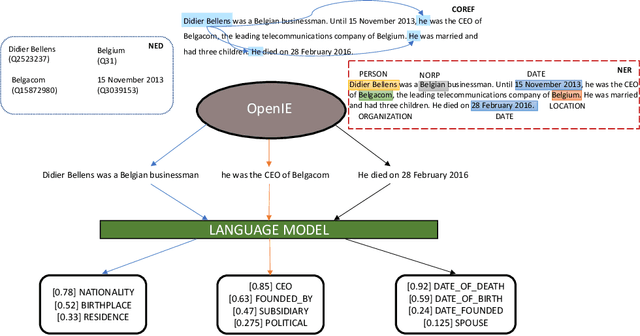
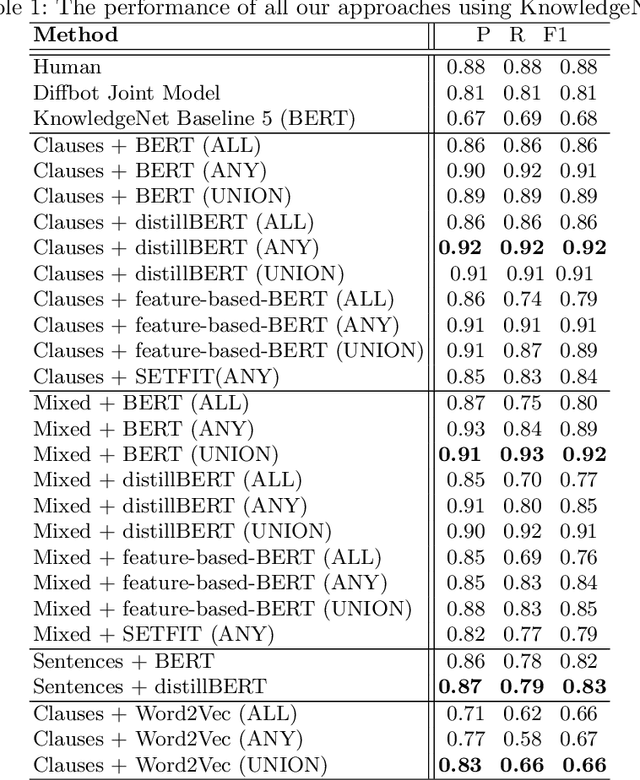
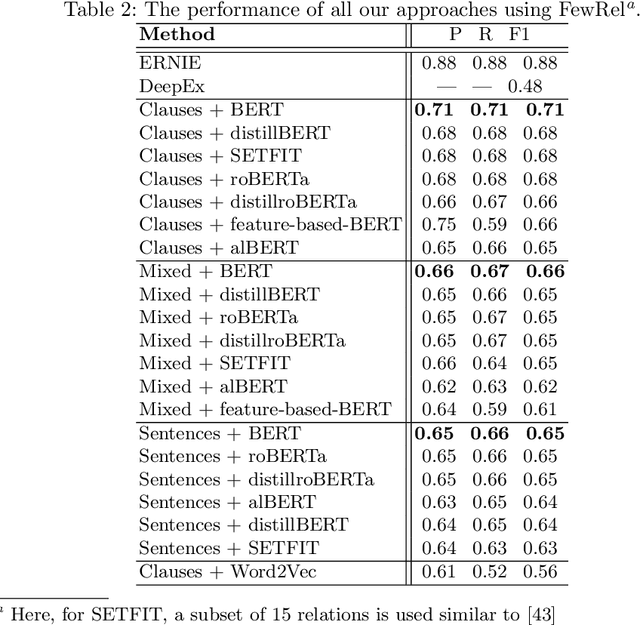
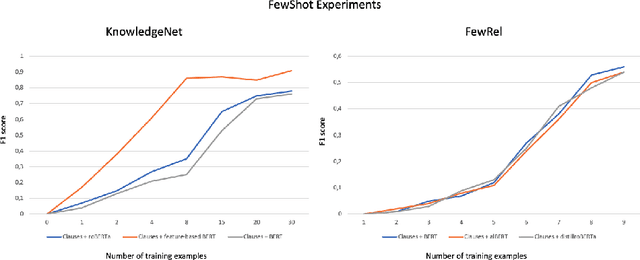
Relation extraction (RE) is a sub-discipline of information extraction (IE) which focuses on the prediction of a relational predicate from a natural-language input unit (such as a sentence, a clause, or even a short paragraph consisting of multiple sentences and/or clauses). Together with named-entity recognition (NER) and disambiguation (NED), RE forms the basis for many advanced IE tasks such as knowledge-base (KB) population and verification. In this work, we explore how recent approaches for open information extraction (OpenIE) may help to improve the task of RE by encoding structured information about the sentences' principal units, such as subjects, objects, verbal phrases, and adverbials, into various forms of vectorized (and hence unstructured) representations of the sentences. Our main conjecture is that the decomposition of long and possibly convoluted sentences into multiple smaller clauses via OpenIE even helps to fine-tune context-sensitive language models such as BERT (and its plethora of variants) for RE. Our experiments over two annotated corpora, KnowledgeNet and FewRel, demonstrate the improved accuracy of our enriched models compared to existing RE approaches. Our best results reach 92% and 71% of F1 score for KnowledgeNet and FewRel, respectively, proving the effectiveness of our approach on competitive benchmarks.

Robust and Provable Guarantees for Sparse Random Embeddings

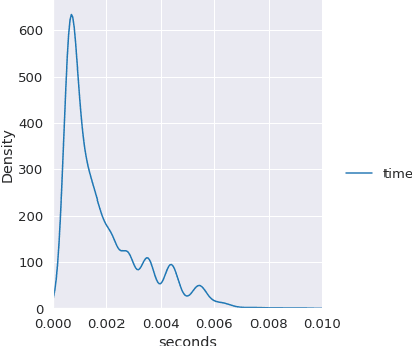
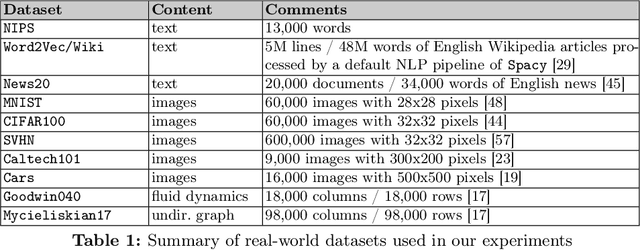
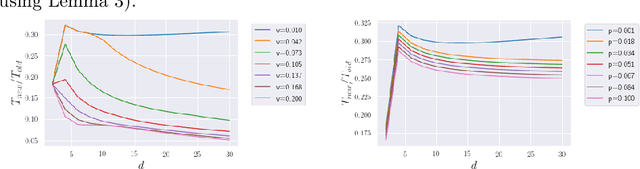
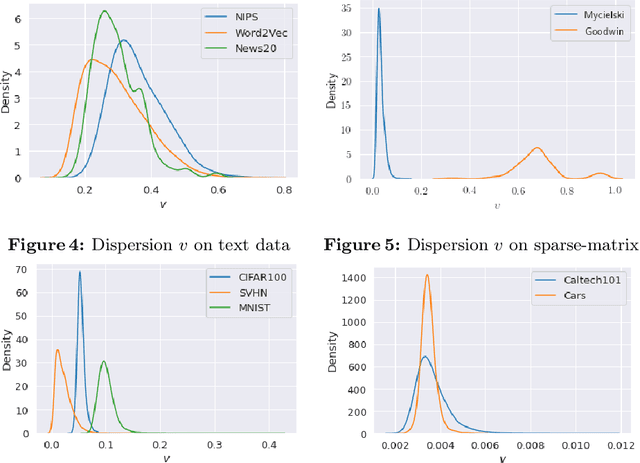
In this work, we improve upon the guarantees for sparse random embeddings, as they were recently provided and analyzed by Freksen at al. (NIPS'18) and Jagadeesan (NIPS'19). Specifically, we show that (a) our bounds are explicit as opposed to the asymptotic guarantees provided previously, and (b) our bounds are guaranteed to be sharper by practically significant constants across a wide range of parameters, including the dimensionality, sparsity and dispersion of the data. Moreover, we empirically demonstrate that our bounds significantly outperform prior works on a wide range of real-world datasets, such as collections of images, text documents represented as bags-of-words, and text sequences vectorized by neural embeddings. Behind our numerical improvements are techniques of broader interest, which improve upon key steps of previous analyses in terms of (c) tighter estimates for certain types of quadratic chaos, (d) establishing extreme properties of sparse linear forms, and (e) improvements on bounds for the estimation of sums of independent random variables.