Mapping the Technological Future: A Topic, Sentiment, and Emotion Analysis in Social Media Discourse

People worldwide are currently confronted with a number of technological challenges, which act as a potent source of uncertainty. The uncertainty arising from the volatility and unpredictability of technology (such as AI) and its potential consequences is widely discussed on social media. This study uses BERTopic modelling along with sentiment and emotion analysis on 1.5 million tweets from 2021 to 2023 to identify anticipated tech-driven futures and capture the emotions communicated by 400 key opinion leaders (KOLs). Findings indicate positive sentiment significantly outweighs negative, with a prevailing dominance of positive anticipatory emotions. Specifically, the 'Hope' score is approximately 10.33\% higher than the median 'Anxiety' score. KOLs emphasize 'Optimism' and benefits over 'Pessimism' and challenges. The study emphasizes the important role KOLs play in shaping future visions through anticipatory discourse and emotional tone during times of technological uncertainty.

What Twitter Data Tell Us about the Future?

Anticipation is a fundamental human cognitive ability that involves thinking about and living towards the future. While language markers reflect anticipatory thinking, research on anticipation from the perspective of natural language processing is limited. This study aims to investigate the futures projected by futurists on Twitter and explore the impact of language cues on anticipatory thinking among social media users. We address the research questions of what futures Twitter's futurists anticipate and share, and how these anticipated futures can be modeled from social data. To investigate this, we review related works on anticipation, discuss the influence of language markers and prestigious individuals on anticipatory thinking, and present a taxonomy system categorizing futures into "present futures" and "future present". This research presents a compiled dataset of over 1 million publicly shared tweets by future influencers and develops a scalable NLP pipeline using SOTA models. The study identifies 15 topics from the LDA approach and 100 distinct topics from the BERTopic approach within the futurists' tweets. These findings contribute to the research on topic modelling and provide insights into the futures anticipated by Twitter's futurists. The research demonstrates the futurists' language cues signals futures-in-the-making that enhance social media users to anticipate their own scenarios and respond to them in present. The fully open-sourced dataset, interactive analysis, and reproducible source code are available for further exploration.

Exact Non-Oblivious Performance of Rademacher Random Embeddings

This paper revisits the performance of Rademacher random projections, establishing novel statistical guarantees that are numerically sharp and non-oblivious with respect to the input data. More specifically, the central result is the Schur-concavity property of Rademacher random projections with respect to the inputs. This offers a novel geometric perspective on the performance of random projections, while improving quantitatively on bounds from previous works. As a corollary of this broader result, we obtained the improved performance on data which is sparse or is distributed with small spread. This non-oblivious analysis is a novelty compared to techniques from previous work, and bridges the frequently observed gap between theory and practise. The main result uses an algebraic framework for proving Schur-concavity properties, which is a contribution of independent interest and an elegant alternative to derivative-based criteria.

Robust and Provable Guarantees for Sparse Random Embeddings

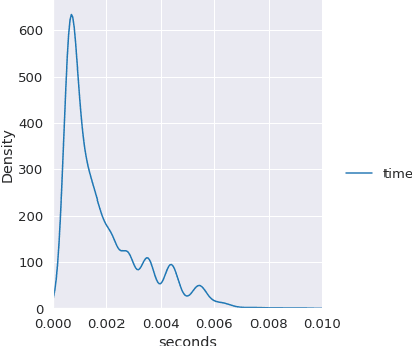
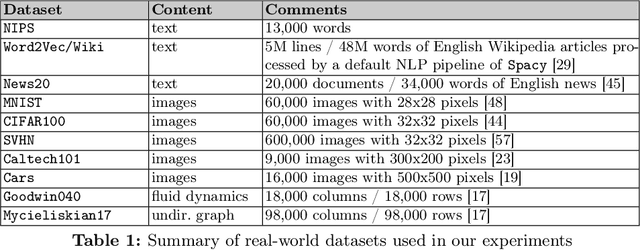
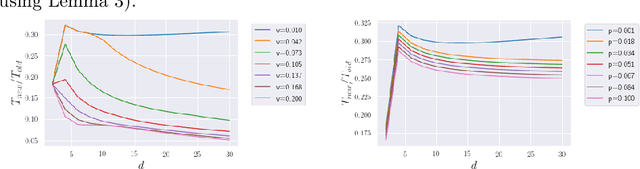
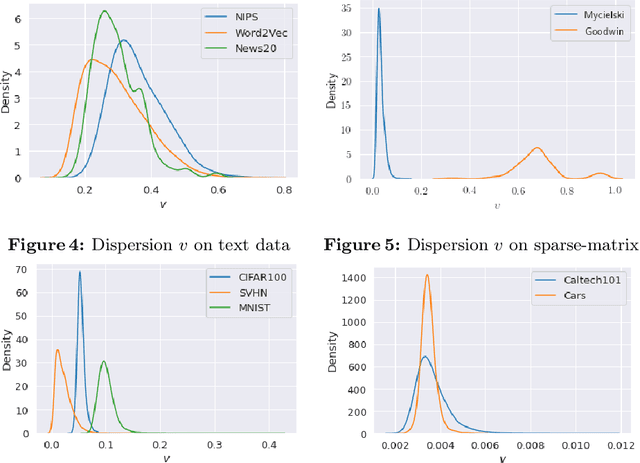
In this work, we improve upon the guarantees for sparse random embeddings, as they were recently provided and analyzed by Freksen at al. (NIPS'18) and Jagadeesan (NIPS'19). Specifically, we show that (a) our bounds are explicit as opposed to the asymptotic guarantees provided previously, and (b) our bounds are guaranteed to be sharper by practically significant constants across a wide range of parameters, including the dimensionality, sparsity and dispersion of the data. Moreover, we empirically demonstrate that our bounds significantly outperform prior works on a wide range of real-world datasets, such as collections of images, text documents represented as bags-of-words, and text sequences vectorized by neural embeddings. Behind our numerical improvements are techniques of broader interest, which improve upon key steps of previous analyses in terms of (c) tighter estimates for certain types of quadratic chaos, (d) establishing extreme properties of sparse linear forms, and (e) improvements on bounds for the estimation of sums of independent random variables.

Mean-Squared Accuracy of Good-Turing Estimator

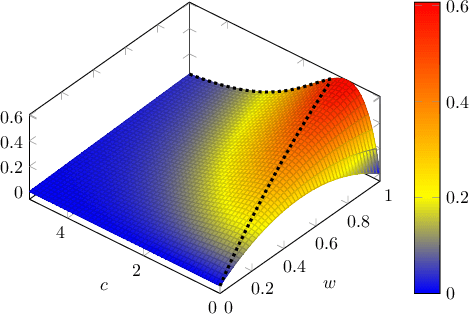
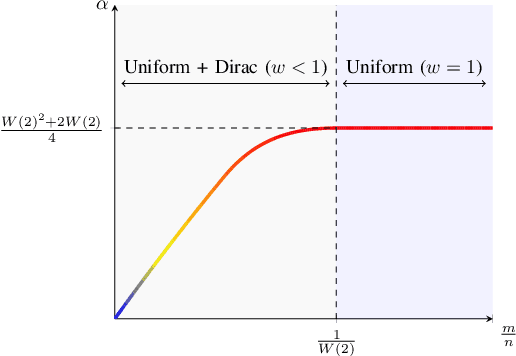
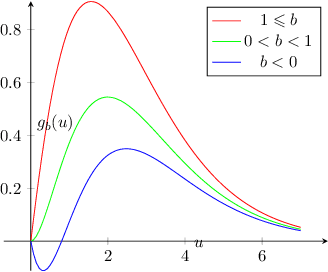
The brilliant method due to Good and Turing allows for estimating objects not occurring in a sample. The problem, known under names "sample coverage" or "missing mass" goes back to their cryptographic work during WWII, but over years has found has many applications, including language modeling, inference in ecology and estimation of distribution properties. This work characterizes the maximal mean-squared error of the Good-Turing estimator, for any sample \emph{and} alphabet size.

Confidence-Optimal Random Embeddings

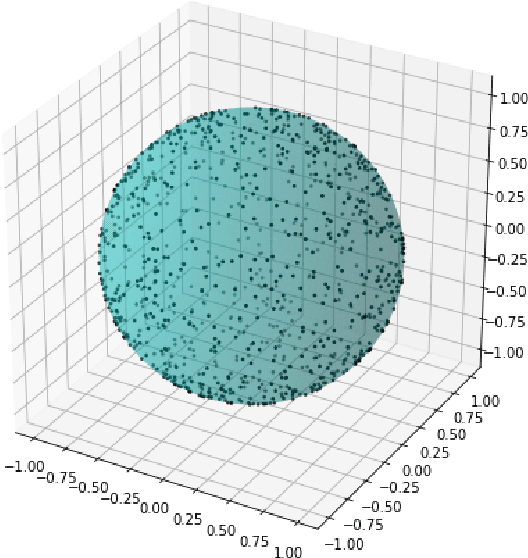
The seminal result of Johnson and Lindenstrauss on random embeddings has been intensively studied in applied and theoretical computer science. Despite that vast body of literature, we still lack of complete understanding of statistical properties of random projections; a particularly intriguing question is: why are the theoretical bounds that far behind the empirically observed performance? Motivated by this question, this work develops Johnson-Lindenstrauss distributions with optimal, data-oblivious, statistical confidence bounds. These bounds are numerically best possible, for any given data dimension, embedding dimension, and distortion tolerance. They improve upon prior works in terms of statistical accuracy, as well as exactly determine the no-go regimes for data-oblivious approaches. Furthermore, the corresponding projection matrices are efficiently samplable. The construction relies on orthogonal matrices, and the proof uses certain elegant properties of the unit sphere. The following techniques introduced in this work are of independent interest: a) a compact expression for distortion in terms of singular eigenvalues of the projection matrix, b) a parametrization linking the unit sphere and the Dirichlet distribution and c) anti-concentration bounds for the Dirichlet distribution. Besides the technical contribution, the paper presents applications and numerical evaluation along with working implementation in Python.

Random Embeddings with Optimal Accuracy

This work constructs Jonson-Lindenstrauss embeddings with best accuracy, as measured by variance, mean-squared error and exponential concentration of the length distortion. Lower bounds for any data and embedding dimensions are determined, and accompanied by matching and efficiently samplable constructions (built on orthogonal matrices). Novel techniques: a unit sphere parametrization, the use of singular-value latent variables and Schur-convexity are of independent interest.

A Modern Analysis of Hutchinson's Trace Estimator

The paper establishes the new state-of-art in the accuracy analysis of Hutchinson's trace estimator. Leveraging tools that have not been previously used in this context, particularly hypercontractive inequalities and concentration properties of sub-gamma distributions, we offer an elegant and modular analysis, as well as numerically superior bounds. Besides these improvements, this work aims to better popularize the aforementioned techniques within the CS community.

Simple Analysis of Johnson-Lindenstrauss Transform under Neuroscience Constraints

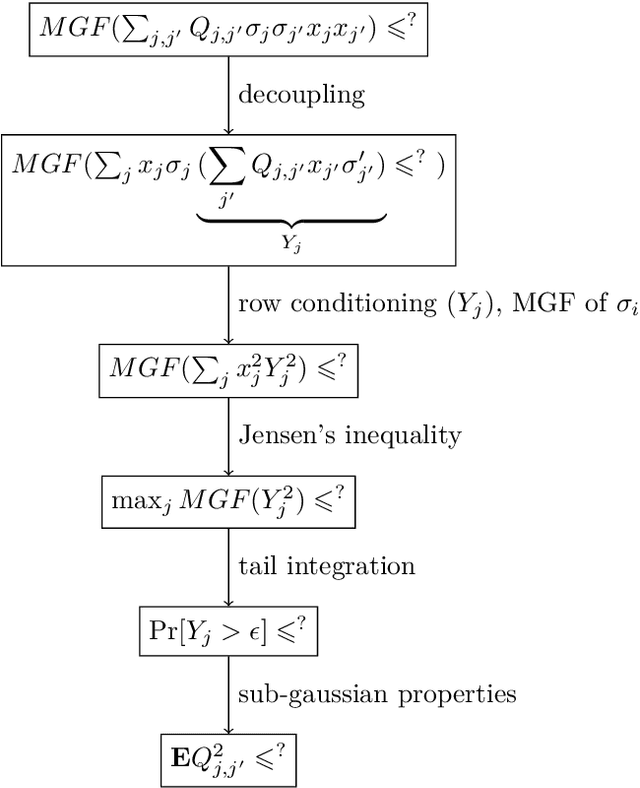
The paper re-analyzes a version of the celebrated Johnson-Lindenstrauss Lemma, in which matrices are subjected to constraints that naturally emerge from neuroscience applications: a) sparsity and b) sign-consistency. This particular variant was studied first by Allen-Zhu, Gelashvili, Micali, Shavit and more recently by Jagadeesan (RANDOM'19). The contribution of this work is a novel proof, which in contrast to previous works a) uses the modern probability toolkit, particularly basics of sub-gaussian and sub-gamma estimates b) is self-contained, with no dependencies on subtle third-party results c) offers explicit constants. At the heart of our proof is a novel variant of Hanson-Wright Lemma (on concentration of quadratic forms). Of independent interest are also auxiliary facts on sub-gaussian random variables.

Revisiting Concentration of Missing Mass

We revisit the problem of \emph{missing mass concentration}, developing a new method of estimating concentration of heterogenic sums, in spirit of celebrated Rosenthal's inequality. As a result we slightly improve the state-of-art bounds due to Ben-Hamou at al., and simplify the proofs.