Mean-Squared Accuracy of Good-Turing Estimator
Paper and Code
Apr 14, 2021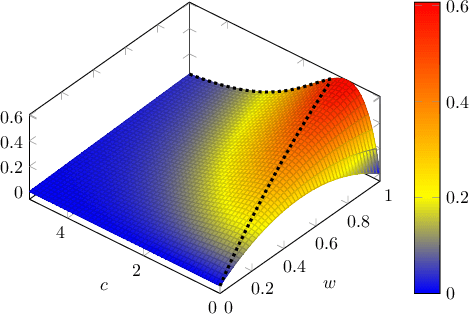
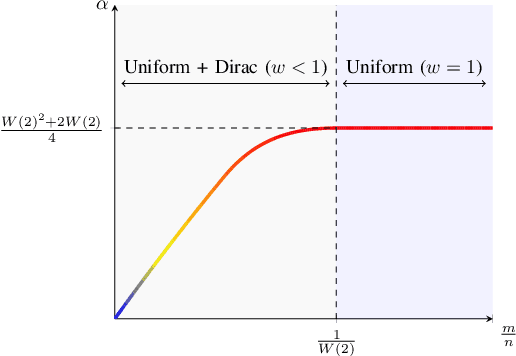
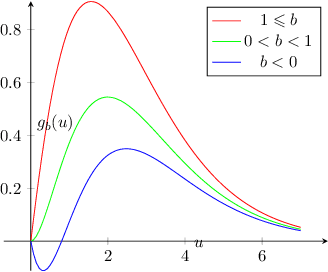
The brilliant method due to Good and Turing allows for estimating objects not occurring in a sample. The problem, known under names "sample coverage" or "missing mass" goes back to their cryptographic work during WWII, but over years has found has many applications, including language modeling, inference in ecology and estimation of distribution properties. This work characterizes the maximal mean-squared error of the Good-Turing estimator, for any sample \emph{and} alphabet size.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge