Knowledge Elicitation via Sequential Probabilistic Inference for High-Dimensional Prediction

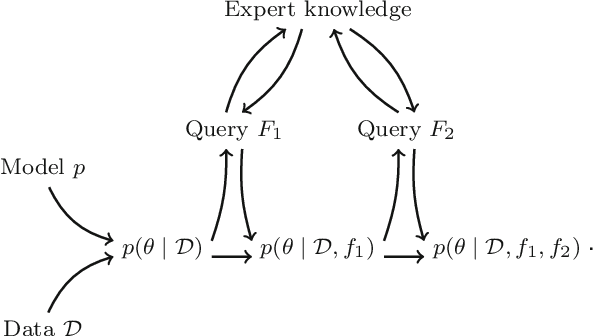
Prediction in a small-sized sample with a large number of covariates, the "small n, large p" problem, is challenging. This setting is encountered in multiple applications, such as precision medicine, where obtaining additional samples can be extremely costly or even impossible, and extensive research effort has recently been dedicated to finding principled solutions for accurate prediction. However, a valuable source of additional information, domain experts, has not yet been efficiently exploited. We formulate knowledge elicitation generally as a probabilistic inference process, where expert knowledge is sequentially queried to improve predictions. In the specific case of sparse linear regression, where we assume the expert has knowledge about the values of the regression coefficients or about the relevance of the features, we propose an algorithm and computational approximation for fast and efficient interaction, which sequentially identifies the most informative features on which to query expert knowledge. Evaluations of our method in experiments with simulated and real users show improved prediction accuracy already with a small effort from the expert.

Improving drug sensitivity predictions in precision medicine through active expert knowledge elicitation

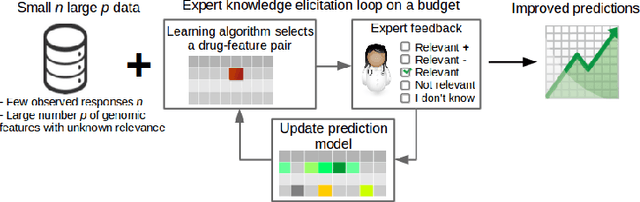
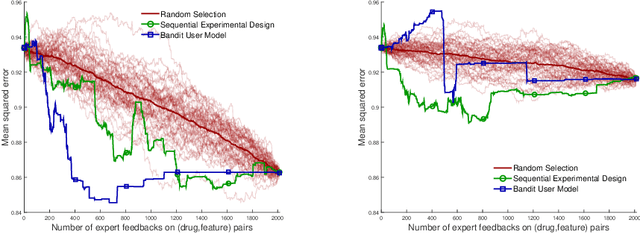
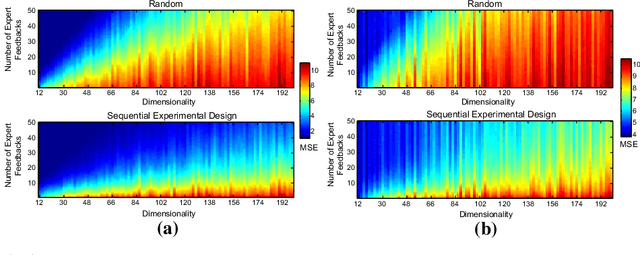
Predicting the efficacy of a drug for a given individual, using high-dimensional genomic measurements, is at the core of precision medicine. However, identifying features on which to base the predictions remains a challenge, especially when the sample size is small. Incorporating expert knowledge offers a promising alternative to improve a prediction model, but collecting such knowledge is laborious to the expert if the number of candidate features is very large. We introduce a probabilistic model that can incorporate expert feedback about the impact of genomic measurements on the sensitivity of a cancer cell for a given drug. We also present two methods to intelligently collect this feedback from the expert, using experimental design and multi-armed bandit models. In a multiple myeloma blood cancer data set (n=51), expert knowledge decreased the prediction error by 8%. Furthermore, the intelligent approaches can be used to reduce the workload of feedback collection to less than 30% on average compared to a naive approach.

Regression with n$\to$1 by Expert Knowledge Elicitation

We consider regression under the "extremely small $n$ large $p$" condition, where the number of samples $n$ is so small compared to the dimensionality $p$ that predictors cannot be estimated without prior knowledge. This setup occurs in personalized medicine, for instance, when predicting treatment outcomes for an individual patient based on noisy high-dimensional genomics data. A remaining source of information is expert knowledge, which has received relatively little attention in recent years. We formulate the inference problem of asking expert feedback on features on a budget, propose an elicitation strategy for a simple "small $n$" setting, and derive conditions under which the elicitation strategy is optimal. Experiments on simulated experts, both on synthetic and genomics data, demonstrate that the proposed strategy can drastically improve prediction accuracy.

Interactive Elicitation of Knowledge on Feature Relevance Improves Predictions in Small Data Sets

Providing accurate predictions is challenging for machine learning algorithms when the number of features is larger than the number of samples in the data. Prior knowledge can improve machine learning models by indicating relevant variables and parameter values. Yet, this prior knowledge is often tacit and only available from domain experts. We present a novel approach that uses interactive visualization to elicit the tacit prior knowledge and uses it to improve the accuracy of prediction models. The main component of our approach is a user model that models the domain expert's knowledge of the relevance of different features for a prediction task. In particular, based on the expert's earlier input, the user model guides the selection of the features on which to elicit user's knowledge next. The results of a controlled user study show that the user model significantly improves prior knowledge elicitation and prediction accuracy, when predicting the relative citation counts of scientific documents in a specific domain.

Best-Arm Identification in Linear Bandits

We study the best-arm identification problem in linear bandit, where the rewards of the arms depend linearly on an unknown parameter $\theta^*$ and the objective is to return the arm with the largest reward. We characterize the complexity of the problem and introduce sample allocation strategies that pull arms to identify the best arm with a fixed confidence, while minimizing the sample budget. In particular, we show the importance of exploiting the global linear structure to improve the estimate of the reward of near-optimal arms. We analyze the proposed strategies and compare their empirical performance. Finally, as a by-product of our analysis, we point out the connection to the $G$-optimality criterion used in optimal experimental design.