Sketches for Time-Dependent Machine Learning

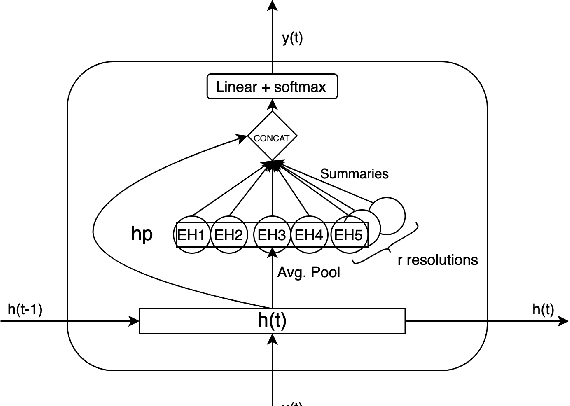
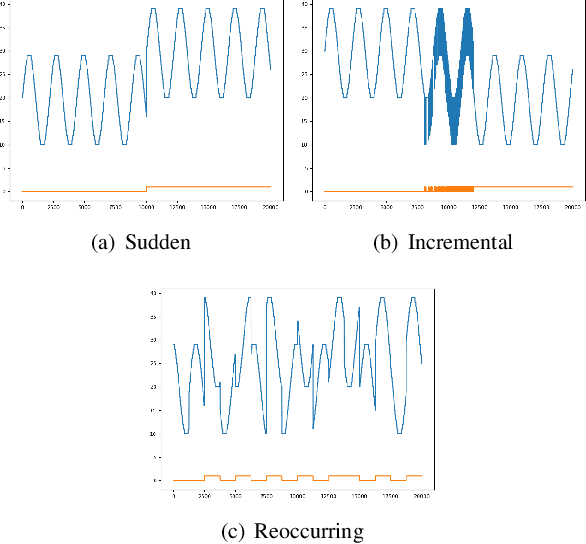
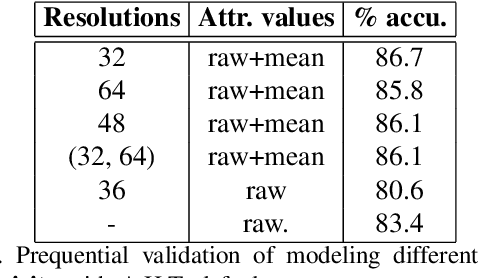
Time series data can be subject to changes in the underlying process that generates them and, because of these changes, models built on old samples can become obsolete or perform poorly. In this work, we present a way to incorporate information about the current data distribution and its evolution across time into machine learning algorithms. Our solution is based on efficiently maintaining statistics, particularly the mean and the variance, of data features at different time resolutions. These data summarisations can be performed over the input attributes, in which case they can then be fed into the model as additional input features, or over latent representations learned by models, such as those of Recurrent Neural Networks. In classification tasks, the proposed techniques can significantly outperform the prediction capabilities of equivalent architectures with no feature / latent summarisations. Furthermore, these modifications do not introduce notable computational and memory overhead when properly adjusted.

Characterizing Transactional Databases for Frequent Itemset Mining

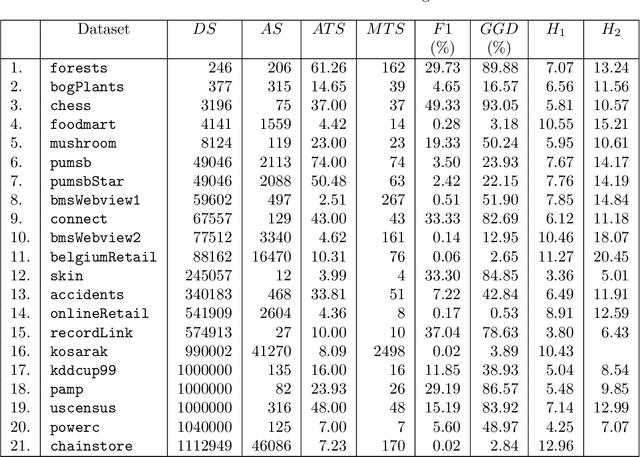
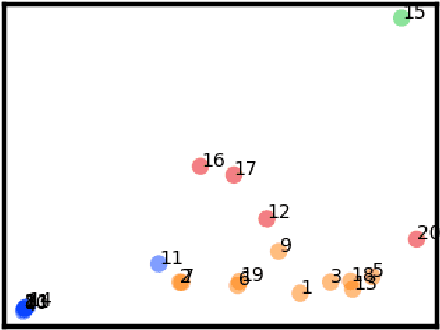
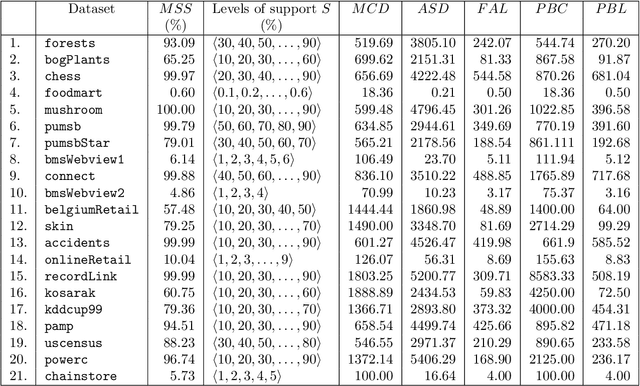
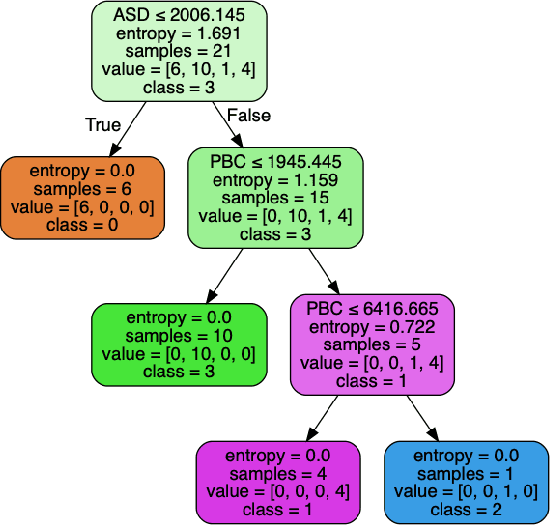
This paper presents a study of the characteristics of transactional databases used in frequent itemset mining. Such characterizations have typically been used to benchmark and understand the data mining algorithms working on these databases. The aim of our study is to give a picture of how diverse and representative these benchmarking databases are, both in general but also in the context of particular empirical studies found in the literature. Our proposed list of metrics contains many of the existing metrics found in the literature, as well as new ones. Our study shows that our list of metrics is able to capture much of the datasets' inner complexity and thus provides a good basis for the characterization of transactional datasets. Finally, we provide a set of representative datasets based on our characterization that may be used as a benchmark safely.

Synthetic Dataset Generation with Itemset-Based Generative Models

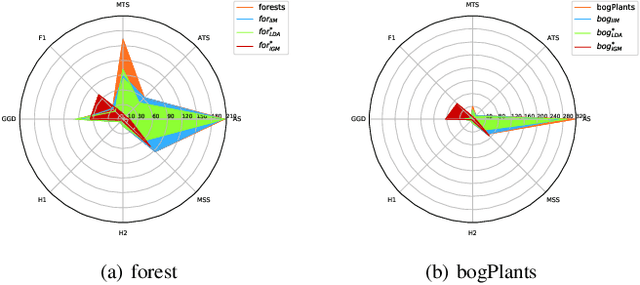
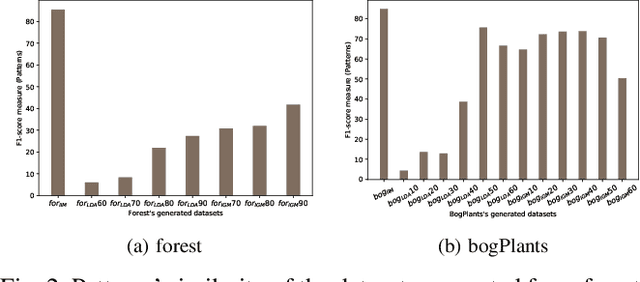
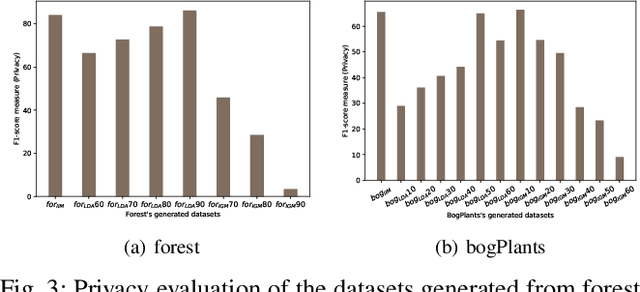
This paper proposes three different data generators, tailored to transactional datasets, based on existing itemset-based generative models. All these generators are intuitive and easy to implement and show satisfactory performance. The quality of each generator is assessed by means of three different methods that capture how well the original dataset structure is preserved.

A Deep-Reinforcement Learning Approach for Software-Defined Networking Routing Optimization

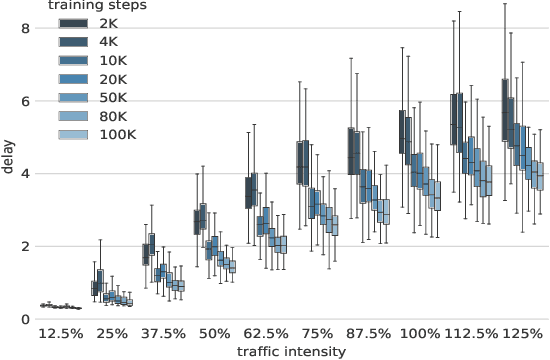
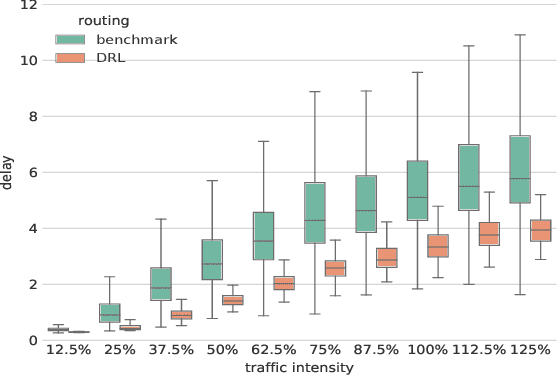
In this paper we design and evaluate a Deep-Reinforcement Learning agent that optimizes routing. Our agent adapts automatically to current traffic conditions and proposes tailored configurations that attempt to minimize the network delay. Experiments show very promising performance. Moreover, this approach provides important operational advantages with respect to traditional optimization algorithms.

Identifiability and Transportability in Dynamic Causal Networks

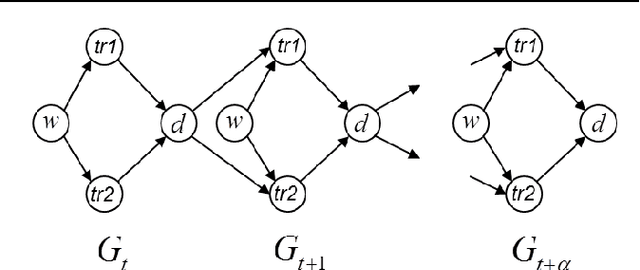
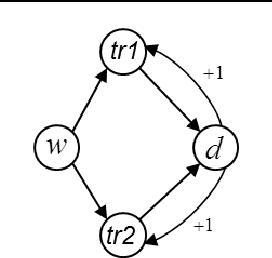
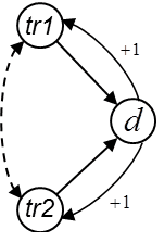
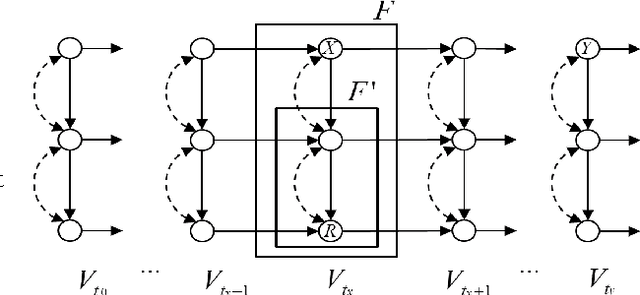
In this paper we propose a causal analog to the purely observational Dynamic Bayesian Networks, which we call Dynamic Causal Networks. We provide a sound and complete algorithm for identification of Dynamic Causal Net- works, namely, for computing the effect of an intervention or experiment, based on passive observations only, whenever possible. We note the existence of two types of confounder variables that affect in substantially different ways the iden- tification procedures, a distinction with no analog in either Dynamic Bayesian Networks or standard causal graphs. We further propose a procedure for the transportability of causal effects in Dynamic Causal Network settings, where the re- sult of causal experiments in a source domain may be used for the identification of causal effects in a target domain.

Learning Definite Horn Formulas from Closure Queries

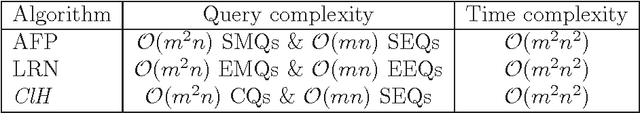
A definite Horn theory is a set of n-dimensional Boolean vectors whose characteristic function is expressible as a definite Horn formula, that is, as conjunction of definite Horn clauses. The class of definite Horn theories is known to be learnable under different query learning settings, such as learning from membership and equivalence queries or learning from entailment. We propose yet a different type of query: the closure query. Closure queries are a natural extension of membership queries and also a variant, appropriate in the context of definite Horn formulas, of the so-called correction queries. We present an algorithm that learns conjunctions of definite Horn clauses in polynomial time, using closure and equivalence queries, and show how it relates to the canonical Guigues-Duquenne basis for implicational systems. We also show how the different query models mentioned relate to each other by either showing full-fledged reductions by means of query simulation (where possible), or by showing their connections in the context of particular algorithms that use them for learning definite Horn formulas.