Relative Entailment Among Probabilistic Implications

We study a natural variant of the implicational fragment of propositional logic. Its formulas are pairs of conjunctions of positive literals, related together by an implicational-like connective; the semantics of this sort of implication is defined in terms of a threshold on a conditional probability of the consequent, given the antecedent: we are dealing with what the data analysis community calls confidence of partial implications or association rules. Existing studies of redundancy among these partial implications have characterized so far only entailment from one premise and entailment from two premises, both in the stand-alone case and in the case of presence of additional classical implications (this is what we call "relative entailment"). By exploiting a previously noted alternative view of the entailment in terms of linear programming duality, we characterize exactly the cases of entailment from arbitrary numbers of premises, again both in the stand-alone case and in the case of presence of additional classical implications. As a result, we obtain decision algorithms of better complexity; additionally, for each potential case of entailment, we identify a critical confidence threshold and show that it is, actually, intrinsic to each set of premises and antecedent of the conclusion.

Learning Definite Horn Formulas from Closure Queries

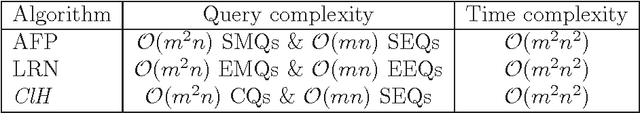
A definite Horn theory is a set of n-dimensional Boolean vectors whose characteristic function is expressible as a definite Horn formula, that is, as conjunction of definite Horn clauses. The class of definite Horn theories is known to be learnable under different query learning settings, such as learning from membership and equivalence queries or learning from entailment. We propose yet a different type of query: the closure query. Closure queries are a natural extension of membership queries and also a variant, appropriate in the context of definite Horn formulas, of the so-called correction queries. We present an algorithm that learns conjunctions of definite Horn clauses in polynomial time, using closure and equivalence queries, and show how it relates to the canonical Guigues-Duquenne basis for implicational systems. We also show how the different query models mentioned relate to each other by either showing full-fledged reductions by means of query simulation (where possible), or by showing their connections in the context of particular algorithms that use them for learning definite Horn formulas.

Closed-set-based Discovery of Bases of Association Rules

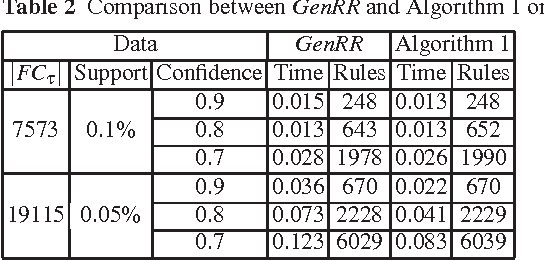
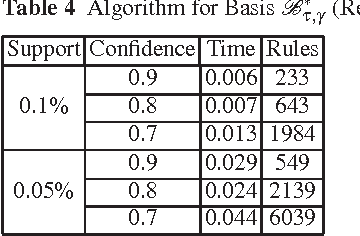
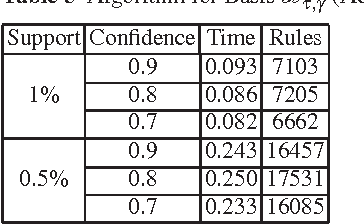
The output of an association rule miner is often huge in practice. This is why several concise lossless representations have been proposed, such as the "essential" or "representative" rules. We revisit the algorithm given by Kryszkiewicz (Int. Symp. Intelligent Data Analysis 2001, Springer-Verlag LNCS 2189, 350-359) for mining representative rules. We show that its output is sometimes incomplete, due to an oversight in its mathematical validation. We propose alternative complete generators and we extend the approach to an existing closure-aware basis similar to, and often smaller than, the representative rules, namely the basis B*.

Formal and Computational Properties of the Confidence Boost of Association Rules

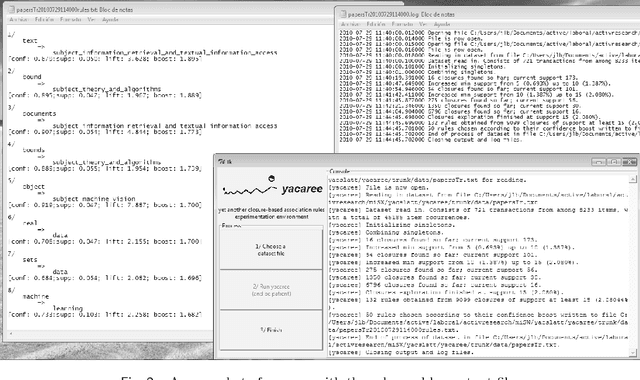
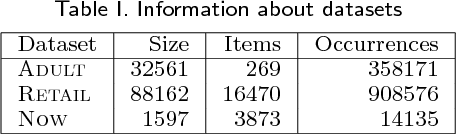
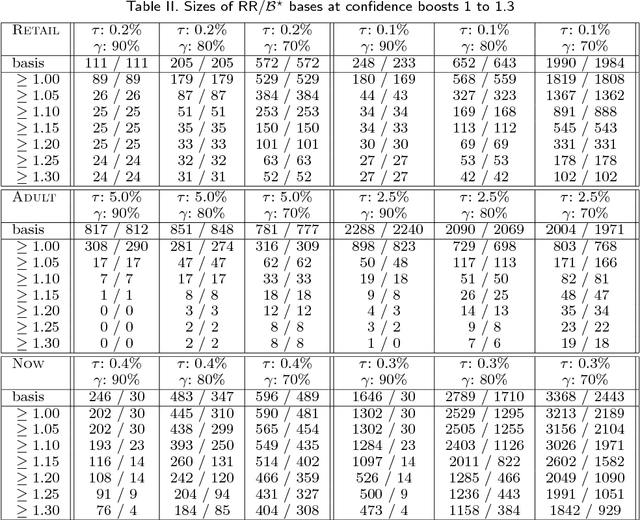
Some existing notions of redundancy among association rules allow for a logical-style characterization and lead to irredundant bases of absolutely minimum size. One can push the intuition of redundancy further and find an intuitive notion of interest of an association rule, in terms of its "novelty" with respect to other rules. Namely: an irredundant rule is so because its confidence is higher than what the rest of the rules would suggest; then, one can ask: how much higher? We propose to measure such a sort of "novelty" through the confidence boost of a rule, which encompasses two previous similar notions (confidence width and rule blocking, of which the latter is closely related to the earlier measure "improvement"). Acting as a complement to confidence and support, the confidence boost helps to obtain small and crisp sets of mined association rules, and solves the well-known problem that, in certain cases, rules of negative correlation may pass the confidence bound. We analyze the properties of two versions of the notion of confidence boost, one of them a natural generalization of the other. We develop efficient algorithmics to filter rules according to their confidence boost, compare the concept to some similar notions in the bibliography, and describe the results of some experimentation employing the new notions on standard benchmark datasets. We describe an open-source association mining tool that embodies one of our variants of confidence boost in such a way that the data mining process does not require the user to select any value for any parameter.

Border Algorithms for Computing Hasse Diagrams of Arbitrary Lattices

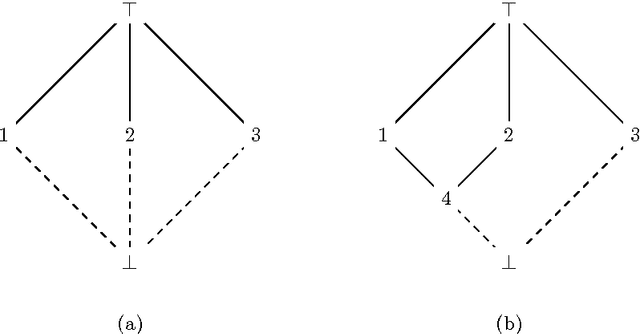
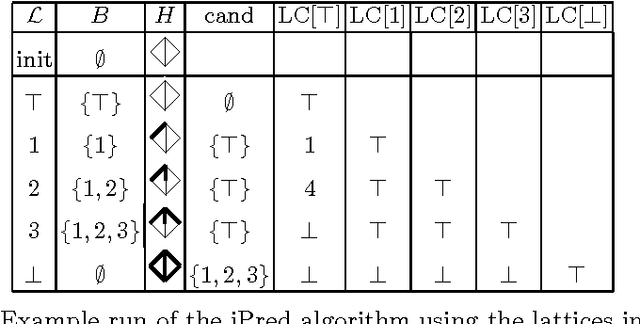
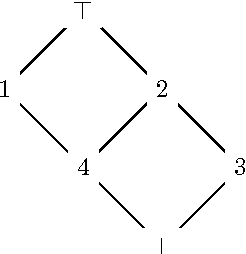
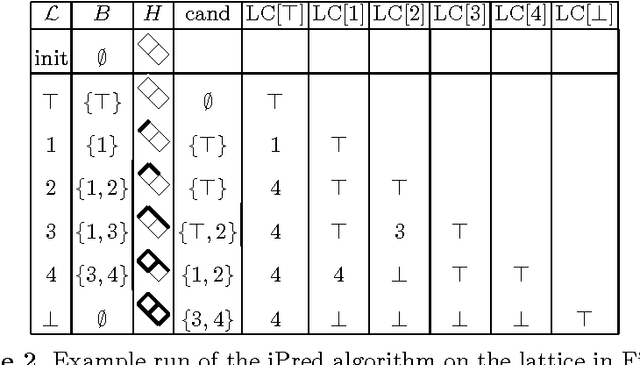
The Border algorithm and the iPred algorithm find the Hasse diagrams of FCA lattices. We show that they can be generalized to arbitrary lattices. In the case of iPred, this requires the identification of a join-semilattice homomorphism into a distributive lattice.